题目内容
3.已知函数f(x)=sin$\frac{πx}{2}$,任取t∈R,若函数f(x)在区间[t,t+2]上的最大值为Mt,最小值为mt,记h(t)=Mt-mt.(1)求h(0)的值,并求出方程h(t)=2的根;
(2)当t∈[-2,2]时,求函数h(t)的解析式.
分析 (1)由题意可得函数的周期为4,由h(0)=M0-m0 求得结果.方程h(t)=2,即Mt-mt=2,即 Mt=1,mt=-1,结合f(x)的图象求得t的值.
(2)当t∈[-2,2]时,分类讨论分别求得Mt和mt的值,可得h(t)=Mt-mt的值.
g(t+4)=Mt-mt=g(t),然后探索-2≤t≤0的函数f(x)的最值,以及g(t)的解析式,即可得到结论.
解答 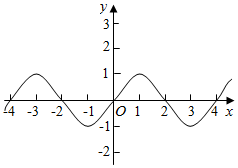 解:(1)函数f(x)=sin$\frac{πx}{2}$,它的最小正周期为$\frac{2π}{\frac{π}{2}}$=4,画出函数f(x)的部图象,
解:(1)函数f(x)=sin$\frac{πx}{2}$,它的最小正周期为$\frac{2π}{\frac{π}{2}}$=4,画出函数f(x)的部图象,
如右图,任取t∈R,若函数f(x)在区间[t,t+2]上的最大值为Mt,最小值为mt,
记h(t)=Mt-mt ,则h(0)=M0-m0=1-0=1.
方程h(t)=2,即Mt-mt=2,即 Mt=1,mt=-1,此时,t=2k+1,k∈Z.
(2)当t∈[-2,2]时,
若-2≤t<-1,Mt=sin($\frac{t+2}{2}π$)=-sin$\frac{π}{2}$t,mt=-1,g(t)=Mt-mt =-sin$\frac{π}{2}$t+1.
若-1≤t<0,Mt=1,mt=sin$\frac{π}{2}$t,g(t)=Mt-mt =1-sin$\frac{π}{2}$t,
若0≤t<1,Mt=1,mt=sin($\frac{t+2}{2}π$)=-sin$\frac{π}{2}$t,g(t)=Mt-mt =1+sin$\frac{π}{2}$t.
若1≤t≤2,Mt=sin$\frac{π}{2}$t,mt=-1,g(t)=Mt-mt =sin$\frac{π}{2}$t+1,
综上可得,函数h(t)=$\left\{\begin{array}{l}{1-sin\frac{π}{2}t,t∈[-2,0)}\\{1+sin\frac{π}{2}t,t∈[0,2]}\end{array}\right.$.
点评 本题主要考查函数的周期性以及应用,根据三角函数的图象和性质写出函数式,综合性较强,难度较大.

| A. | $\frac{2}{5}$ | B. | -$\frac{6}{37}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{2}{3}$ |
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5}{6}π$ |
| A. | [-$\sqrt{3}$,+∞) | B. | (-∞,$\sqrt{3}$] | C. | [-$\sqrt{3}$,3) | D. | [-$\sqrt{3}$,+$\sqrt{3}$] |
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{6}}{2}$ |
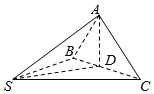 如图所示,在四面体S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=60°,∠BSC=90°,D是BC的中点.求证:
如图所示,在四面体S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=60°,∠BSC=90°,D是BC的中点.求证: