题目内容
如果点M（x，y）在运动过程中总满足关系式
+
=10，点M的轨迹是什么曲线？为什么？写出它的方程．
| (x+4)2+y2 |
| (x-4)2+y2 |
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据
+
=10，可得（x，y）与（-4，0），（4，0）的距离之和等于常数10，由椭圆的定义可知点M的轨迹，从而可得椭圆的方程．
| (x+4)2+y2 |
| (x-4)2+y2 |
解答：
解：∵
+
=10，
∴（x，y）与（-4，0），（4，0）的距离之和等于常数10，
由椭圆的定义可知：此点的轨迹为焦点在x轴上的椭圆，且a=5，c=4
∴b=3，
故椭圆的方程为：
+
=1．
| (x+4)2+y2 |
| (x-4)2+y2 |
∴（x，y）与（-4，0），（4，0）的距离之和等于常数10，
由椭圆的定义可知：此点的轨迹为焦点在x轴上的椭圆，且a=5，c=4
∴b=3，
故椭圆的方程为：
| x2 |
| 25 |
| y2 |
| 9 |
点评：本题考查椭圆的标准方程，着重考查椭圆的定义的应用，考查转化思想与运算能力，属于中档题．
练习册系列答案
相关题目
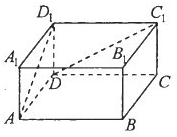如图，在长方体ABCD-A1B1C1D1中，底面是边长为2的正方形，高为1，则异面直线AD1和DC1所成角的余弦值等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
双曲线
-
=1的渐近线方程是（ ）
| y2 |
| 9 |
| x2 |
| 16 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
已知函数y=sinx（x∈R）的图象如图所示，则t的值是（ ）
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
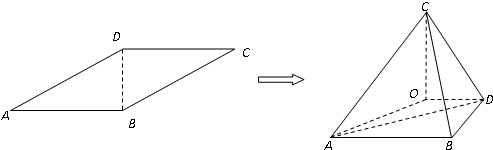
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示．