题目内容
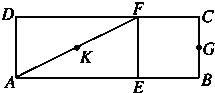 如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为
如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为AF的中点.沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为考点:点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:先作出二面角A-EF-B的平面角,再利用余弦定理,即可求得结论.
解答:
解:由题设知,△ADF为直角三角形,K为△ADF的外心,则K为AF的中点,
取EF中点H,连接KH、HG、KG.
∵K、H分别为FA,FE的中点,
∴KH∥AE.

又AE⊥EF,∴KH⊥EF.
又GH⊥EF,
∴∠KHG即为二面角A-EF-B的平面角,
∴∠KHG=120°.
在△KHG中,KH=
AE=1,GH=1,
∴KG=
=
故答案为:
取EF中点H,连接KH、HG、KG.
∵K、H分别为FA,FE的中点,
∴KH∥AE.

又AE⊥EF,∴KH⊥EF.
又GH⊥EF,
∴∠KHG即为二面角A-EF-B的平面角,
∴∠KHG=120°.
在△KHG中,KH=
| 1 |
| 2 |
∴KG=
| 1+1-2×1×1×cos120° |
| 3 |
故答案为:
| 3 |
点评:本题考查面面角,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
若某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、32 | B、16 | C、24 | D、48 |
