题目内容
已知圆C：x2+y2-2x+4y-4=0，
（Ⅰ）若过定点（-2，0）的直线l与圆C相切，求直线l的方程；
（Ⅱ）若过定点（-1，0）且倾斜角为
的直线l与圆C相交于A，B两点，求线段AB的中点P的坐标．
（Ⅰ）若过定点（-2，0）的直线l与圆C相切，求直线l的方程；
（Ⅱ）若过定点（-1，0）且倾斜角为
| π |
| 6 |
考点：直线与圆锥曲线的综合问题
专题：综合题,直线与圆
分析：（I）当直线l的斜率不存在时，直线x=-2与⊙C相切，因此直线x=-2是圆的一条切线；当直线l的斜率存在时，设切线方程为y=k（x+2），则圆心C到切线l的距离d=r．利用点到直线的距离公式得出k即可；
（II）设A（x1，y1），B（x2，y2）．过定点（-1，0）且倾斜角为
的直线l方程为y=
（x+1），与圆的方程联立化为关于x的一元二次方程的根与系数的关系，利用中点坐标公式即可得出．
（II）设A（x1，y1），B（x2，y2）．过定点（-1，0）且倾斜角为
| π |
| 6 |
| ||
| 3 |
解答：
解：（I）圆C：（x-1）2+（y+2）2=9．得到圆心C（1，-2），半径r=3．
当直线l的斜率不存在时，直线x=-2与⊙C相切，因此直线x=-2是圆的一条切线；
当直线l的斜率存在时，设切线方程为y=k（x+2），则圆心C到切线l的距离d=r．
∴
=3，解得k=
．
∴切线l的方程为y=
（x+2），即5x-12y+10=0．
综上可知：切线l的方程为x=-2或5x-12y+10=0．
（II）设A（x1，y1），B（x2，y2）．
过定点（-1，0）且倾斜角为
的直线l方程为y=
（x+1）．
代入圆方程可化为4x2+（4
-4）x+4
-11=0，
∴x1+x2=1-
，
∴xP=
=
，yP=
（
+1）=
．
∴P（
，
）．
当直线l的斜率不存在时，直线x=-2与⊙C相切，因此直线x=-2是圆的一条切线；
当直线l的斜率存在时，设切线方程为y=k（x+2），则圆心C到切线l的距离d=r．
∴
| |k+2+2k | ||
|
| 5 |
| 12 |
∴切线l的方程为y=
| 5 |
| 12 |
综上可知：切线l的方程为x=-2或5x-12y+10=0．
（II）设A（x1，y1），B（x2，y2）．
过定点（-1，0）且倾斜角为
| π |
| 6 |
| ||
| 3 |
代入圆方程可化为4x2+（4
| 3 |
| 3 |
∴x1+x2=1-
| 3 |
∴xP=
| x1+x2 |
| 2 |
1-
| ||
| 2 |
| ||
| 3 |
1-
| ||
| 2 |
| ||
| 2 |
∴P（
1-
| ||
| 2 |
| ||
| 2 |
点评：本题综合考查了直线与圆的位置关系转化为方程联立得到△与0的关系、根与系数的关系、圆的切线的性质、中点坐标公式等基础知识与基本技能方法，属于中档题．
练习册系列答案
相关题目
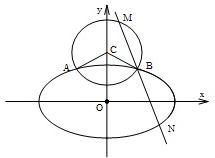已知离心率为
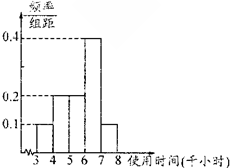节能灯的质量通过其正常使用时间来衡量，使用时间越长，表明治疗越好．若使用时间小于4千小时的产品为不合格产品；使用时间在4千小时到6千小时（不含6千小时）的产品为合格品；使用时间大于或等于6千小时的产品为优质品．某节能灯生产厂家为了解同一类型号的某批次产品的质量情况，随机抽取了部分产品作为样本，得到实验结果的频率直方图如图所示．若上述实验结果中使用时间落入各组的频率作为相应的概率．