题目内容
18.若数列{an}的前n项和为Sn,且Sn=2an+1,则an=-2n-1.分析 利用递推关系与等比数列的通项公式即可得出.
解答 解:∵Sn=2an+1,
∴当n=1时,a1=2a1+1,解得a1=-1.
当n≥2时,an=Sn-Sn-1=2an+1-(2an-1+1),
化为an=2an-1,
∴数列{an}是等比数列,首项为-1.公比为2.
∴an=-2n-1.
故答案为:-2n-1.
点评 本题考查了递推关系与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
6.已知偶函数f(x)在(-∞,0]上单调递减,f(-1)=0,若f(log2x)<0,则x的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | (-∞,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(2,+∞) | D. | (0,2) |
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0,且关于x的函数f(x)=2x3-3|$\overrightarrow{a}$|x2+6$\overrightarrow{a}$•$\overrightarrow{b}$x+5在实数集R上有极值,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的取值范围是( )
| A. | ($\frac{π}{3}$,π) | B. | ($\frac{π}{3}$,π] | C. | [$\frac{π}{3}$,π] | D. | (0,$\frac{π}{3}$) |
3.等差数列{an}中,a3=2,a5=7,则a7=( )
| A. | 10 | B. | 20 | C. | 16 | D. | 12 |
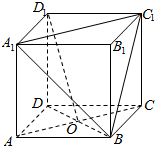 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.