题目内容

3．等差数列{an}中，a3=2，a5=7，则a7=（　　）
A．10B．20C．16D．12

分析 设出等差数列的公差，由已知求出公差，再代入等差数列的通项公式得答案．

解答 解：设等差数列{an}的公差为d，
由a3=2，a5=7，得$d=\frac{{a}_{5}-{a}_{3}}{5-3}=\frac{7-2}{2}=\frac{5}{2}$．
∴${a}_{7}={a}_{5}+2d=7+2×\frac{5}{2}=12$．
故选：D．

点评 本题考查等差数列的通项公式，是基础的计算题．

练习册系列答案
相关题目
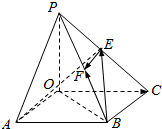11．如图，四棱锥P-OABC的底面为一矩形，PO⊥平面OABC．设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OC}$=$\overrightarrow{b}$，$\overrightarrow{OP}$=$\overrightarrow{c}$，E，F分别是PC和PB的中点，用$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$．
12．已知圆心为C的圆，满足下列条件：圆心C位于x轴正半轴上，与直线3x-4y+7=0相切，且被y轴截得的弦长为2$\sqrt{3}$，圆C的面积小于13．
（1）求圆C的标准方程；
（2）一条光线从点A（4，1）出发，经直线y=x-5反射后与圆C相切，求入射光线所在直线的斜率．
11．若两个函数的图象有一个公共点，并在该点处的切线相同，就说这两个函数有why点．已知函数f（x）=lnx和g（x）=em•ex有why点，则m所在的区间为（　　）
A．$（{-2，-\frac{3}{2}}）$B．$（{-\frac{3}{2}，-1}）$C．$（{-\frac{5}{2}，-2}）$D．$（{-1，-\frac{1}{3}}）$
18．若数列{an}的前n项和为Sn，且Sn=2an+1，则an=-2n-1．
8．在几何体①圆锥；②正方体；③圆柱；④球；⑤正四面体中，三视图完全一样的是②④．
15．已知函数$f（x）=\frac{{\sqrt{3}}}{2}sin2x-{cos^2}x+\frac{3}{4}（x∈R）$
（1）当$x∈[{-\frac{π}{12}，\frac{5π}{12}}]$时，求函数f（x）的最小值和最大值；
（2）若x=x0$（{0≤{x_0}≤\frac{π}{2}}）$为f（x）的一个零点，求sin2x0的值．
12．若椭圆${C_1}：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点（2，1），离心率为$\frac{{\sqrt{2}}}{2}$，F1，F2分别为其左、右焦点．
（1）若点P与F1，F2的距离之比为$\frac{1}{3}$，求直线$x-\sqrt{2}y+\sqrt{3}=0$被点P所在的曲线C2截得的弦长；
（2）设A1，A2分别为椭圆C1的左、右顶点，Q为C1上异于A1，A2的任意一点，直线A1Q交C1的右准线于点M，直线A2Q交C1的右准线于点N，试问$\overrightarrow{M{F_2}}•\overrightarrow{N{F_2}}$是否为定值，若是，求出其定值，若不是，说明理由．
13．已知集合A={1，3}，B={0，1，a}，A∪B={0，1，3}，则a=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网