题目内容
6.已知偶函数f(x)在(-∞,0]上单调递减,f(-1)=0,若f(log2x)<0,则x的取值范围是( )| A. | ($\frac{1}{2}$,2) | B. | (-∞,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(2,+∞) | D. | (0,2) |
分析 根据题意,利用函数的奇偶性和单调性之间的关系,将不等式f(log2x)<0进行转化-1<log2x<1,利用对数函数的性质解可得x的范围,即可得答案.
解答 解:∵偶函数f(x)在(-∞,0]上单调递减,∴f(x)在[0,+∞)上单调递增,
又∵f(x)为偶函数,则f(1)=f(-1)=0,
∴不等式f(log2x)>0等价为-1<log2x<1,
解可得:$\frac{1}{2}$<x<2,
即不等式的解集为($\frac{1}{2}$,2),
故选:A.
点评 本题考查函数的奇偶性与单调性的综合运用,涉及对数函数的性质,利用函数的奇偶性的定义将不等式进行转化是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列各组向量中不平行的是( )
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,4) | B. | $\overrightarrow{c}$=(1,0,0),$\overrightarrow{d}$=(-3,0,0) | ||
| C. | $\overrightarrow{e}$=(2,3,0),$\overrightarrow{f}$=(0,0,0) | D. | $\overrightarrow{g}$=(-2,3,5)$\overrightarrow{h}$=(16,-24,40) |
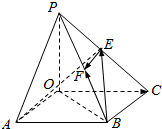 如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.