题目内容
8.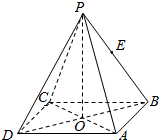 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
分析 取AD中点M,连接MO,PM,连接AE,OE,由OE∥PD,知∠OEA为异面直线PD与AE所成的角.由此能求出异面直线PD与AE所成角的正切值.
解答 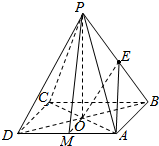 解:取AD中点M,连接MO,PM,依条件可知AD⊥MO,AD⊥PO,∵PO⊥面ABCD,
解:取AD中点M,连接MO,PM,依条件可知AD⊥MO,AD⊥PO,∵PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∵侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,∴tan∠PAO=$\frac{\sqrt{6}}{2}$.
设AB=a,则AO=$\frac{\sqrt{2}}{2}$a,
∴PO=AO•tan∠POA=$\frac{\sqrt{3}}{2}a$a,
连接AE,OE,∵OE∥PD,∴∠OEA为异面直线PD与AE所成的角.
∵AO⊥BD,AO⊥PO,∴AO⊥平面PBD.又OE?平面PBD,∴AO⊥OE.
∵OE=$\frac{1}{2}$PD=$\frac{1}{2}\sqrt{P{O}^{2}+D{O}^{2}}$=$\frac{5}{4}$a,
∴tan∠AEO=$\frac{AO}{EO}$=$\frac{2\sqrt{10}}{5}$.
故选:A.
点评 本题考查异面直线所成角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.两条平行线3x+4y-12=0与ax+8y-4=0之间的距离为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.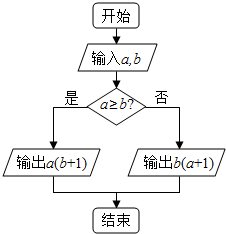 对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
 对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )| A. | 8 | B. | 15 | C. | 16 | D. | $\frac{3}{2}$ |