题目内容
3．设集合P={x|$\int_0^x{（{3{t^2}-10t+6}）}dt$=0}，则集合P的所有子集个数是（ ）| A． | 2 | B． | 3 | C． | 7 | D． | 8 |
分析 先根据定积分求出集合P，根据集合子集的公式2n（其中n为集合的元素），求出集合A的子集个数．
解答 解：$\int_0^x{（{3{t^2}-10t+6}）}dt$=（t3-5t2+6t）|${\;}_{0}^{x}$=x3-5x2+6x=x（x-2）（x-3）=0，解得x=0，或2，或3，
∴P={0，2，3}，
∴集合P的所有子集个数23=8，
故选：D．
点评 此题考查学生掌握子集与真子集的定义，会利用2n求集合的子集，是一道基础题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
13．教室内有一根直尺，无论怎样放置，在地面上总有这样的直线，它与直尺所在直线（ ）
| A． | 垂直 | B． | 异面 | C． | 平行 | D． | 相交 |
8．
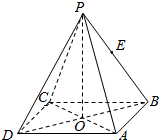如图所示，正四棱锥P-ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$，若E是PB的中点，则异面直线PD与AE所成角的正切值为（ ）
如图所示，正四棱锥P-ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$，若E是PB的中点，则异面直线PD与AE所成角的正切值为（ ）| A． | $\frac{{2\sqrt{10}}}{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\sqrt{5}$ | D． | $\frac{{\sqrt{10}}}{5}$ |