题目内容
18.若圆的方程为${(x+\frac{k}{2})^2}+{(y+1)^2}=1-\frac{3}{4}{k^2}$,则当圆的面积最大时,圆心坐标和半径分别为(0,-1)、1.分析 把圆的方程化为标准式方程后,找出圆心坐标与半径,要求圆的面积最大即要圆的半径的平方最大,所以根据平方的最小值为0即k=0时得到半径的平方最大,所以把k=0代入圆心坐标中即可得到此时的圆心坐标.
解答 解:∵圆的方程为${(x+\frac{k}{2})^2}+{(y+1)^2}=1-\frac{3}{4}{k^2}$.
∴r2=1-$\frac{3}{4}$k2>0,rmax=1,此时k=0.
∴圆心为(0,-1).
故答案为:(0,-1),1.
点评 本题以二次函数的最值问题为平台考查学生掌握圆的标准方程并会根据圆的标准方程找出圆心和半径,是一道基础题.

练习册系列答案
相关题目
9.方程xlnx-2=0的解所在的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
13.教室内有一根直尺,无论怎样放置,在地面上总有这样的直线,它与直尺所在直线( )
| A. | 垂直 | B. | 异面 | C. | 平行 | D. | 相交 |
8.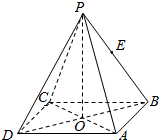 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
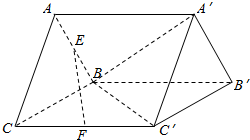 已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.