题目内容
16．两条平行线3x+4y-12=0与ax+8y-4=0之间的距离为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 路平行关系求出a，然后求解平行线之间的距离．
解答 解：两条平行线3x+4y-12=0与ax+8y-4=0，可得a=6，
平行线之间的距离为：$\frac{|12-2|}{\sqrt{{3}^{2}+{4}^{2}}}$=2．
故选：B．
点评 本题考查平行线之间的距离的求法，是基础题．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
8．
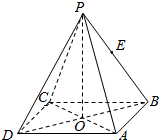如图所示，正四棱锥P-ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$，若E是PB的中点，则异面直线PD与AE所成角的正切值为（ ）
如图所示，正四棱锥P-ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$，若E是PB的中点，则异面直线PD与AE所成角的正切值为（ ）| A． | $\frac{{2\sqrt{10}}}{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\sqrt{5}$ | D． | $\frac{{\sqrt{10}}}{5}$ |