题目内容
13.已知函数f(1-2x)=4x2+2x,则f(3)=2.分析 直接利用函数的解析式求解函数值即可.
解答 解:函数f(1-2x)=4x2+2x,则f(3)=f(1-2×(-1))
=4-2=2
故答案为:2.
点评 本题考查函数的解析式的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
8.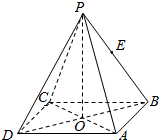 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
18.设i 是虚数单位,复数$\frac{2i}{1+i}$对应的点与原点的距离是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
2.如果一个几何体的主(正)视图,左(侧)视图,俯视图都是全等的图形,那么称这个几何体为“完美几何体”.在下面选项中,可以由“完美几何体”组成的选项是( )
| A. | 正方体、球、侧棱两两垂直且相等的正三棱锥 | |
| B. | 正方体、球、各棱长都相等的正三棱柱 | |
| C. | 球、高和底面半径相等的圆柱、高和底面半径相等的圆锥 | |
| D. | 正方体、正四棱台、棱长相等的平行六面体 |
3.f(x)=$\left\{\begin{array}{l}-\frac{2}{x},x<0\\ 3+log_2x,x>0\end{array}$若f(x)=2,则x=( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | -1或1 | D. | -1或$\frac{1}{2}$ |
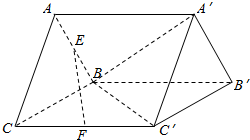 已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.
已知三棱柱ABC-A′B′C′如图所示,四边形BCC′B′为菱形,∠BCC′=60°,△ABC为等边三角形,面ABC⊥面BCC′B′,E、F分别为棱AB、CC′的中点.