题目内容
已知函数f(x)=sin
cos
+
cos2
.
(Ⅰ)求该函数图象的对称轴;
(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2=ac,求f(B)的取值范围.
| x |
| 3 |
| x |
| 3 |
| 3 |
| x |
| 3 |
(Ⅰ)求该函数图象的对称轴;
(Ⅱ)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2=ac,求f(B)的取值范围.
考点:两角和与差的正弦函数,正弦函数的对称性,余弦定理
专题:高考数学专题,三角函数的图像与性质
分析:(Ⅰ)利用两角和与差的三角函数,化简函数为一个角的一个三角函数的形式,然后求该函数图象的对称轴;
(Ⅱ)通过在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2=ac,利用余弦定理求出B 地方我,得到相位的范围,即可求解f(B)的取值范围.
(Ⅱ)通过在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2=ac,利用余弦定理求出B 地方我,得到相位的范围,即可求解f(B)的取值范围.
解答:
解:(Ⅰ)f(x)=
sin
+
(1+cos
)=
sin
+
cos
+
=sin(
+
)+
由sin(
+
)=±1即
+
=kπ+
(k∈z)得x=(
+
)π
即对称轴为x=(
+
)π
…(6分)
(Ⅱ)由已知b2=ac,∴cosB=
=
≥
=
,
∴
≤cosB<1,
∴0<B≤
,
∴
<
+
≤
,
∴
<sin(
+
)≤1
∴
<sin(
+
)+
≤1+
,
即f(B)的值域为(
,1+
].…(14分)
| 1 |
| 2 |
| 2x |
| 3 |
| ||
| 2 |
| 2x |
| 3 |
| 1 |
| 2 |
| 2x |
| 3 |
| ||
| 2 |
| 2x |
| 3 |
| ||
| 2 |
| 2x |
| 3 |
| π |
| 3 |
| ||
| 2 |
由sin(
| 2x |
| 3 |
| π |
| 3 |
| 2x |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 3k |
| 2 |
| 1 |
| 4 |
|
即对称轴为x=(
| 3k |
| 2 |
| 1 |
| 4 |
|
(Ⅱ)由已知b2=ac,∴cosB=
| a2+c2-b2 |
| 2ac |
| a2+c2-ac |
| 2ac |
| 2ac-ac |
| 2ac |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴0<B≤
| π |
| 3 |
∴
| π |
| 3 |
| 2B |
| 3 |
| π |
| 3 |
| 5π |
| 9 |
∴
| ||
| 2 |
| 2B |
| 3 |
| π |
| 3 |
∴
| 3 |
| 2B |
| 3 |
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
即f(B)的值域为(
| 3 |
| ||
| 2 |
点评:本题考查两角和与差的三角函数,三角函数的图象与性质的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题:“能被4整除的数一定是偶数”,其等价命题( )
| A、偶数一定能被4整除 |
| B、不是偶数不一定能被4整除 |
| C、不能被4整除的数不一定是偶数 |
| D、不是偶数一定不能被4整除 |
函数f(x)=
的定义域是( )
| ||
| x-1 |
| A、[-1,1) |
| B、[-1,1)∪(1,+∞) |
| C、[-1,+∞) |
| D、(1,+∞) |
已知{an}是等差数列,其前n项和为Sn,若a3=7-a2,则S4=( )
| A、15 | B、14 | C、13 | D、12 |
下列函数与y=-x是同一函数的是( )
A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
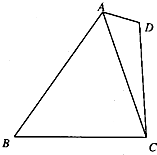 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=