题目内容
过点M(1,2)的直线l与圆C:(x-2)2+y2=9交于A、B两点,C为圆心,当点C到直线l的距离最大时,直线l的方程为( )
| A、x=1 |
| B、y=1 |
| C、x-y+1=0 |
| D、x-2y+3=0 |
考点:直线与圆的位置关系
专题:直线与圆
分析:判断点C到直线l的距离最大时的特征,求出仔细的斜率,然后求解直线方程.
解答:
解:点C到直线l的距离d≤|CM|,当l⊥CM时,点C到直线l的距离
最大,所以kCM•kl=-1.又kCM=
=-2,所以kl=
.
所以直线l的方程为y-2=
(x-1).即x-2y+3=0.
故选D.
最大,所以kCM•kl=-1.又kCM=
| 2-0 |
| 1-2 |
| 1 |
| 2 |
所以直线l的方程为y-2=
| 1 |
| 2 |
故选D.
点评:本题考查与圆的位置关系的应用,直线方程的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(
+1)6(
-1)4的展开式中x的系数是( )
| x |
| x |
| A、-3 | B、3 | C、-4 | D、4 |
x2-3x-10>0的解集为( )
| A、(-∞,2)∪(5,+∞) |
| B、(-2,5) |
| C、(-∞,-2)∪(5+∞) |
| D、(-5,2) |
定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈(-1,0]时,f(x)的值域为( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[0,
|
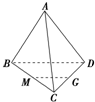
如图所示空间四边形ABCD,连接AC、BD,设M、G分别是BC、CD的中点,则
-
+
等于( )
| MG |
| AB |
| AD |

A、
| ||||
B、3
| ||||
C、3
| ||||
D、2
|
已知函数f(x)=
若0<x1<x2<1,则( )
| 1-x2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、前三个判断都不正确 |