题目内容
若命题p:2n-1(n∈Z)是奇数;q:2n+1(n∈Z)是偶数,则下列说法中正确的是( )
| A、¬p为真 | B、¬q为假 |
| C、p∨q为真 | D、p∧q为真 |
考点:复合命题的真假
专题:简易逻辑
分析:先判定命题p,q的真假,再利用复合命题的判定方法即可得出.
解答:
解:∵命题p:2n-1(n∈Z)是奇数,是真命题;
命题q:2n+1(n∈Z)是偶数,是假命题.
∴p∨q为真.
故选:C.
命题q:2n+1(n∈Z)是偶数,是假命题.
∴p∨q为真.
故选:C.
点评:本题考查了复合命题的判定方法,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
甲乙两人从4门课程中各选修两门,则甲乙所选的课程中至少有1门不相同的选法共有( )种.
| A、30 | B、36 | C、60 | D、72 |
若双曲线
-
=1(a>0,b>0)的一条渐近线为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
已知sin(π+α)=
,α为第三象限角,则tanα=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
执行如图所示的算法,则输出的结果是( )


| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
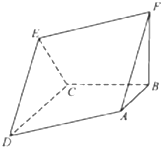 如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.
如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.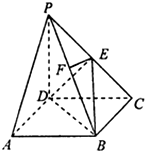 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB,垂足为F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB,垂足为F.