题目内容
 四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点
四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点(1)求证:QP⊥AC;
(2)当二面角Q-AC-P的大小为120°时,求QB的长.
考点:二面角的平面角及求法,棱锥的结构特征
专题:空间位置关系与距离,空间角
分析:(1)由已知得PD⊥AC,AC⊥BD,从而AC⊥平面PDBQ,由此能证明AC⊥PQ.
(2)设AC和BD的交点为O,连结OP,OQ,则∠POD是二面角P-AC-D的平面角,∠POQ是二面角P-AC-Q的平面角,∠POQ=120°,由此利用余弦定理能求出QB.
(2)设AC和BD的交点为O,连结OP,OQ,则∠POD是二面角P-AC-D的平面角,∠POQ是二面角P-AC-Q的平面角,∠POQ=120°,由此利用余弦定理能求出QB.
解答:
(1)证明:∵PD⊥面ABCD,AC?面ABCD,∴PD⊥AC,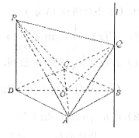
又菱形ABCD中,两对角线垂直,即AC⊥BD,又BD∩PD=D,
∴AC⊥平面PDBQ,∴AC⊥PQ.
(2)解:△PAC和△QAC都是以AC为底的等腰三角形,
设AC和BD的交点为O,连结OP,OQ,
则∠POD是二面角P-AC-D的平面角,
由tan∠POD=
<
,得二面角P-AC-B大小120°,
∴点Q与点P在平面ABCD的同侧,如图所示,
∴∠POQ是二面角P-AC-Q的平面角,∴∠POQ=120°,
在Rt△POD中,OP=
,设QB=x,
则Rt△OBQ中,OQ=
,
在直角梯形PDBQ中,PQ=
=
,
在△POQ中,由余弦定理得PQ=
=6-4x,
故6-4x>0,且3x2-16x+5=0,
解得x=
,即QB=
.

又菱形ABCD中,两对角线垂直,即AC⊥BD,又BD∩PD=D,
∴AC⊥平面PDBQ,∴AC⊥PQ.
(2)解:△PAC和△QAC都是以AC为底的等腰三角形,
设AC和BD的交点为O,连结OP,OQ,
则∠POD是二面角P-AC-D的平面角,
由tan∠POD=
| 2 | ||
|
| 3 |
∴点Q与点P在平面ABCD的同侧,如图所示,
∴∠POQ是二面角P-AC-Q的平面角,∴∠POQ=120°,
在Rt△POD中,OP=
| 7 |
则Rt△OBQ中,OQ=
| x2+3 |
在直角梯形PDBQ中,PQ=
(2-x)2+(2
|
| x2-4x+16 |
在△POQ中,由余弦定理得PQ=
| 7(x 2+3) |
故6-4x>0,且3x2-16x+5=0,
解得x=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查异面直线垂直的证明,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知曲线C的方程是(x-
)2+(y-
)2=8,若点P,Q在曲线C上,则|PQ|的最大值是( )
| |x| |
| x |
| |y| |
| y |
A、6
| ||
B、8
| ||
| C、8 | ||
| D、6 |
甲乙两人从4门课程中各选修两门,则甲乙所选的课程中至少有1门不相同的选法共有( )种.
| A、30 | B、36 | C、60 | D、72 |
已知sin(π+α)=
,α为第三象限角,则tanα=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
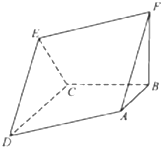 如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.
如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.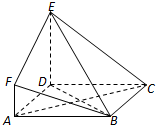 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.