题目内容
求下列函数的定义域:
(1)y=
;
(2)y=lg(3x-2).
(1)y=
| 2-x |
(2)y=lg(3x-2).
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数的解析式,列出使解析式有意义的不等式,求出解集即可.
解答:
解:(1)∵y=
,
∴2-x≥0,
解得x≤2,…(3分)
∴函数y的定义域是(-∞,2];…(3分)
(2)∵y=lg(3x-2),
∴3x-2>0,
解得x>
,…(3分)
∴函数y=lg(3x-2)的定义域是(
,+∞).…(3分)
| 2-x |
∴2-x≥0,
解得x≤2,…(3分)
∴函数y的定义域是(-∞,2];…(3分)
(2)∵y=lg(3x-2),
∴3x-2>0,
解得x>
| 2 |
| 3 |
∴函数y=lg(3x-2)的定义域是(
| 2 |
| 3 |
点评:本题考查了根据函数解析式求函数定义域的问题,是基础题目.

练习册系列答案
相关题目
设i为虚数单位,复数
的共轭复数是( )
| 2i |
| 1-2i |
A、
| ||||
B、-
| ||||
| C、i | ||||
D、-
|
已知函数f(2x)=log2
,则f(1)=( )
| 6x+13 |
| 4 |
A、log2
| ||
B、
| ||
| C、1 | ||
| D、2 |
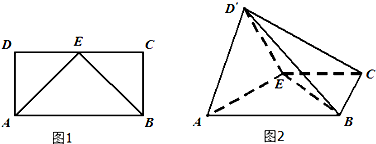
 如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.
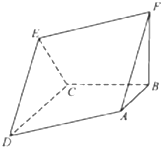
如图所示,四边形ADEF为平行四边形,直线FB⊥平面ABCD,AB∥DC,AB⊥BC,AB=BC=FB=1,CD=2.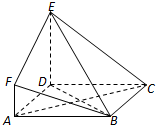 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.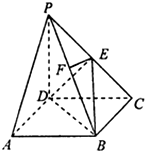 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB,垂足为F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB,垂足为F.