题目内容
已知函数f(x)=lnx+ax2-2bx(a,b∈R),g(x)=
-clnx.
(1)当a=
,b≤1时,f(x)与g(x)在定义域上单调性相反,求的|b|+c的最小值.
(2)当b>
>0时,求证:存在m∈R,使f(x)=m有三个不同的实数解t1,t2,t3,且对任意i,j∈{1,2,3}且i≠j都有
<2b-a(ti+tj).
| 2x-2 |
| x+1 |
(1)当a=
| 1 |
| 2 |
(2)当b>
| 2a |
| 2 |
| ti+tj |
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)当a=
,b≤1时,利用导数可判断f(x)在(0,+∞)上为增函数,从而知g(x)在(0,+∞)上为减函数,于是g′(x)≤0对x∈(0,+∞)恒成立,分离参数c后转化为函数的最值解决,利用基本不等式可求得最值;
(2)利用导数可求f(x)的极值点、单调区间,由单调性极值可知m的存在性;不妨设ti<tj,易知f(ti)=f(tj),即lnti+ati2-2bti=lntj+atj2-2btj,化简可得
ln
=-a(ti+tj)+2b,通过作差可及差的符号可得结论;
| 1 |
| 2 |
(2)利用导数可求f(x)的极值点、单调区间,由单调性极值可知m的存在性;不妨设ti<tj,易知f(ti)=f(tj),即lnti+ati2-2bti=lntj+atj2-2btj,化简可得
| 1 |
| ti-tj |
| ti |
| tj |
解答:
解析:(1)∵f′(x)=
,g′(x)=
.
当a=
时,f′(x)=
;当b≤1时,x2-2bx+1≥0对x∈(0,+∞)恒成立,
∴f′(x)≥0对x∈(0,+∞)恒成立,f(x)在(0,+∞)上为增函数.
根据f(x)和g(x)在定义域上单调性相反得,g(x)在(0,+∞)上为减函数,
∴g′(x)≤0对x∈(0,+∞)恒成立,即:4x≤c(x+1)2,∴c≥
,
∵
≤
=1,当且仅当x=1时,
取最大值1.
∴c≥1,此时|b|+c的最小值是1.
(2)∵f′(x)=
,
当b>
>0时,a>0,且一元二次方程2ax2-2bx+1=0的△=4(b2-2a)>0,
∴2ax2-2bx+1=0有两个不相等的实根x1=
,x2=
,
当x∈(0,x1)时,f(x)为增函数;f(x)∈(-∞,f(x1)),
当x∈(x1,x2)时,f(x)为减函数;f(x)∈(f(x2),f(x1)),
当x∈(x2,+∞)时,f(x)为增函数;f(x)∈(f(x2),+∞),
∴当m∈(f(x2),f(x1))时,f(x)=m一定有3个不相等的实根t1,t2,t3,分别在(-∞,x1)、(x1,x2)、(x2,+∞)内,
不妨设ti<tj,则f(ti)=m,f(tj)=m,
∴f(ti)=f(tj),即lnti+ati2-2bti=lntj+atj2-2btj,即lnti-lntj=-a(ti2-tj2)+2b(ti-tj),即
ln
=-a(ti+tj)+2b,
∴
-[2b-a(ti+tj)]=
-
ln
=
[
-ln
]=
[
-ln
],
令
=t,则
-ln
=
-lnt,
由(1)知g(x)=
-lnx在(0,+∞)上为减函数,又g(1)=0,
∴当0<t<1,
-lnt>0,又
<0,
∴
-[2b-a(ti+tj)]<0,即
<2b-a(ti+tj).
| 2ax2-2bx+1 |
| x |
| -cx2+2(2-c)x-c |
| x(x+1)2 |
当a=
| 1 |
| 2 |
| x2-2bx+1 |
| x |
∴f′(x)≥0对x∈(0,+∞)恒成立,f(x)在(0,+∞)上为增函数.
根据f(x)和g(x)在定义域上单调性相反得,g(x)在(0,+∞)上为减函数,
∴g′(x)≤0对x∈(0,+∞)恒成立,即:4x≤c(x+1)2,∴c≥
| 4x |
| (x+1)2 |
∵
| 4x |
| (x+1)2 |
| 4x | ||
(2
|
| 4x |
| (x+1)2 |
∴c≥1,此时|b|+c的最小值是1.
(2)∵f′(x)=
| 2ax2-2bx+1 |
| x |
当b>
| 2a |
∴2ax2-2bx+1=0有两个不相等的实根x1=
b-
| ||
| 2a |
b+
| ||
| 2a |
当x∈(0,x1)时,f(x)为增函数;f(x)∈(-∞,f(x1)),
当x∈(x1,x2)时,f(x)为减函数;f(x)∈(f(x2),f(x1)),
当x∈(x2,+∞)时,f(x)为增函数;f(x)∈(f(x2),+∞),
∴当m∈(f(x2),f(x1))时,f(x)=m一定有3个不相等的实根t1,t2,t3,分别在(-∞,x1)、(x1,x2)、(x2,+∞)内,
不妨设ti<tj,则f(ti)=m,f(tj)=m,
∴f(ti)=f(tj),即lnti+ati2-2bti=lntj+atj2-2btj,即lnti-lntj=-a(ti2-tj2)+2b(ti-tj),即
| 1 |
| ti-tj |
| ti |
| tj |
∴
| 2 |
| ti+tj |
| 2 |
| ti+tj |
| 1 |
| ti-tj |
| ti |
| tj |
| 1 |
| ti-tj |
| 2(ti-tj) |
| ti+tj |
| ti |
| tj |
| 1 |
| ti-tj |
2(
| ||
|
| ti |
| tj |
令
| ti |
| tj |
2(
| ||
|
| ti |
| tj |
| 2(t-1) |
| t+1 |
由(1)知g(x)=
| 2x-2 |
| x+1 |
∴当0<t<1,
| 2(t-1) |
| t+1 |
| 1 |
| ti-tj |
∴
| 2 |
| ti+tj |
| 2 |
| ti+tj |
点评:该题考查利用导数研究函数的单调性、极值和函数的零点,考查学生综合运用知识分析解决问题的能力,该题运算量大,综合性强,能力要求高.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
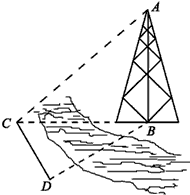 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.