Question

18．已知函数f（x）=x²+mx-|1-x²|（m∈R）．
（1）若m=3，求函数f（x）的单调区间；
（2）若f（x）在区间（0，2）上有且只有1个零点，求实数m的取值范围．

Answer 1

分析 （1）求出f（x）的解析式并化简，根据函数类型判断f（x）的单调区间；
（2）分离参数得$m\;=\frac{{|1-{x^2}|}}{x}-x$，作出其函数图象，根据函数图象得出m的范围．

解答 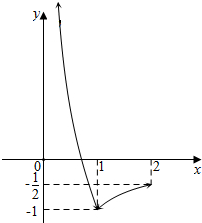解：（1）当m=3时，f（x）=x²+3x-|1-x²|．
①当-1≤x≤1时，$f（x）=2{x^2}+3x-1=2{（x+\frac{3}{4}）^2}-\frac{17}{8}$．
∴f（x）在$（-1，-\frac{3}{4}）$递减，在$（-\frac{3}{4}，1）$递增．
②当x＜-1或x＞1时，f（x）=3x+1．
∴f（x）在（-∞，-1）和（1，+∞）递增．
综上，f（x）的单调递增区间为（-∞，-1）和$（-\frac{3}{4}，+∞）$，单调递减区间为$（-1，-\frac{3}{4}）$．
（2）∵f（x）在区间（0，2）上有且只有1个零点，
∴方程x²+mx-|1-x²|=0在区间（0，2）上有且只有1解，
即方程$m\;=\frac{{|1-{x^2}|}}{x}-x$在区间（0，2）上有且只有1解，
从而函数$y=\frac{{|1-{x^2}|}}{x}-x，x∈（0，2）$图象与直线y=m有且只有一个公共点．
作出函数$y=\left\{{\begin{array}{l}{\frac{1}{x}-2x，}&{0＜x＜1}\\{-\frac{1}{x}，}&{1≤x＜2}\end{array}}\right.$的图象，
结合图象知实数m的取值范围是：$m≥-\frac{1}{2}$或m=-1．

点评 本题考查了分段函数的单调性与单调区间，分段函数的零点个数判断．属于中档题．