题目内容
4.若复数z满足2$\overline{z}$-1=3+6i(i是虚数单位),则z=2-3i.分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:∵2$\overline{z}$-1=3+6i,
∴$2\overline{z}=4+6i$,则$\overline{z}=2+3i$,
∴z=2-3i.
故答案为:2-3i.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.

练习册系列答案
相关题目
14.命题p:2017是奇数,q:2016是偶数,则下列说法中正确的是( )
| A. | p或q为真 | B. | p且q为假 | C. | 非p为真 | D. | 非q为真 |
15.已知直线l:mx+y-1=0(m∈R)是圆C:x2+y2-4x+2y+1=0的对称轴,过点A(-2,m)作圆C的一条切线,切点为B,则|AB|为( )
| A. | 4 | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | 3 |
12.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤0}\\{-lnx,x>0}\end{array}\right.$若关于x的方程f2(x)+f(x)+m=0有三个不同实数根,则m的取值范围是( )
| A. | $m<\frac{1}{4}$ | B. | m≤-2 | C. | $-2≤m<\frac{1}{4}$ | D. | m>2 |
16.过正方体中心的平面截正方体所得的截面中,不可能的图形是( )
| A. | 三角形 | B. | 长方形 | ||
| C. | 对角线不相等的菱形 | D. | 六边形 |




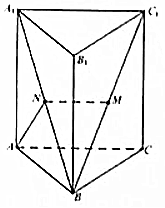 如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.