题目内容

16．过正方体中心的平面截正方体所得的截面中，不可能的图形是（　　）
A．三角形B．长方形
C．对角线不相等的菱形D．六边形

分析 根据截面经过几个面得到的截面就是几边形判断即可．

解答 解：过正方体中心的平面截正方体所得的截面，至少与正方体的四个面相交，所以不可能是三角形，
故选：A．

点评 解决本题的关键是理解截面经过几个面得到的截面就是几边形．

练习册系列答案
相关题目
6．给出以下命题：
①若方程x2+2x+m=0有实根，则m≤2；
②若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的一条渐近线斜率为2，则其离心率为$\sqrt{5}$；
③已知回归直线的斜率的估计值为1.2，样本点的中心为（4，5），则回归直线方程为$\hat y=1.2x+0.2$；
④秦九韶算法的特点在于把求一个n次多项式的值转化为求n个一次多项式的值；
⑤直线l：y=kx+1与圆O：x2+y2=1相交于A，B两点，则“k=1”是“△OAB的面积为$\frac{1}{2}$”必要不充分条件．
其中正确的命题序号为①②③④．
7．若过点M（1，1）的直线l与圆（x-2）2+y2=4相较于两点A，B，且M为弦的中点AB，则|AB|为（　　）
A．$2\sqrt{2}$B．4C．$\sqrt{2}$D．2
4．若复数z满足2$\overline{z}$-1=3+6i（i是虚数单位），则z=2-3i．
11．设椭圆$\frac{x^2}{2}+{y^2}=1$的左、右焦点分别为F1、F2，点P在该椭圆上，则使得△F1F2P是等腰三角形的点P的个数是6．
1．向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$•（$\overrightarrow{a}$+$\overrightarrow{b}$）=0，则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为（　　）
A．$\frac{1}{2}$B．$-\frac{1}{2}$C．0D．$-\frac{{\sqrt{3}}}{2}$
8．以下四个命题中，正确命题的个数是（　　）
①命题“若x=y，则sinx=siny”的逆否命题是真命题；
②已知α，β是不同的平面，m，n是不同的直线，m∥α，n∥β，α⊥β，则m⊥n；
③直线l1：2ax+y+1=0，l2：x+2ay+2=0，l1∥l2的充要条件是$a=\frac{1}{2}$；
④$\int_{-1}^1{sinxdx=0}$．
A．1B．2C．3D．4
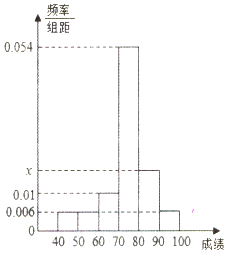5．宿州市教体局为了了解2017届高三毕业生学生情况，利用分层抽样抽取50位学生数学学业水平测试成绩作调查，制作了成绩频率分布直方图，如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）．
（Ⅰ）求图中x的值；
（Ⅱ）根据直方图估计宿州市2017届高三毕业生数学学业水平测试成绩的平均分；
（Ⅲ）在抽取的50人中，从成绩在[50，60）和[90，100]的学生中随机选取2人，求这2人成绩差别不超过10分的概率．
6．已知△ABC的内角A，B，C的对边分别为a，b，c，a2+b2=λab．
（1）若$λ=\sqrt{6}$，$B=\frac{5π}{6}$，求sinA；
（2）若λ=4，AB边上的高为$\frac{{\sqrt{3}c}}{6}$，求C．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网