题目内容
14.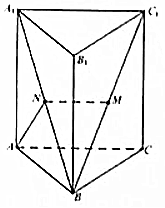 如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.(1)求证:直线AN⊥平面A1BC;
(2)若M在线段BC1上,且MN∥平面A1B1C1,求证:M是BC1的中点.
分析 (1)证明AN⊥BC,AN⊥A1B,即可证明直线AN⊥平面A1BC;
(2)证明MN∥A1C1,利用 N是A1B的中点,可得结论.
解答 证明:(1)∵直三棱柱ABC-A1B1C1,
∴AA1⊥平面ABC,BC?平面ABC,∴AA1⊥BC,
∵AB⊥BC,AA1∩AB=A,
∴BC⊥平面A1AB,…(3分)
∵AN?平面A1AB,
∴AN⊥BC,
∵AA1=AB,且 N是A1B的中点,
∴AN⊥A1B,
∵A1B∩BC=B,
∴直线AN⊥平面A1BC…(7分)
(2)证明:∵MN∥平面A1B1C1,
∴MN∥A1C1,
∵N是A1B的中点,
∴M是BC1的中点…(14分)
点评 本题考查线面垂直的判定与性质,考查线面平行的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
19.若复数z满足(3+4i)z=25,则复平面内表示z的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知集合A={x|x2-2x<0},$B=\left\{{x\left|{-\sqrt{3}<x<\sqrt{3}}\right.}\right\}$,则A∩B=( )
| A. | $\left\{{x\left|{-\sqrt{3}<x<0}\right.}\right\}$ | B. | $\left\{{x\left|{-\sqrt{3}<x<2}\right.}\right\}$ | C. | $\left\{{x\left|{0<x<\sqrt{3}}\right.}\right\}$ | D. | {x|-2<x<0} |
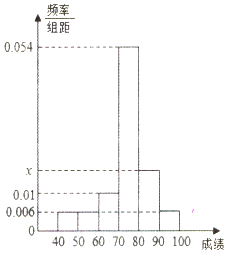 宿州市教体局为了了解2017届高三毕业生学生情况,利用分层抽样抽取50位学生数学学业水平测试成绩作调查,制作了成绩频率分布直方图,如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100).
宿州市教体局为了了解2017届高三毕业生学生情况,利用分层抽样抽取50位学生数学学业水平测试成绩作调查,制作了成绩频率分布直方图,如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100).