题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤0}\\{-lnx,x>0}\end{array}\right.$若关于x的方程f2(x)+f(x)+m=0有三个不同实数根,则m的取值范围是( )| A. | $m<\frac{1}{4}$ | B. | m≤-2 | C. | $-2≤m<\frac{1}{4}$ | D. | m>2 |
分析 结合方程f2(x)+f(x)+m=0有三个不同的实数根,将问题转化为函数图象交点的个数判断问题,结合函数f(x)的图象即可获得解答.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤0}\\{-lnx,x>0}\end{array}\right.$的图象如图,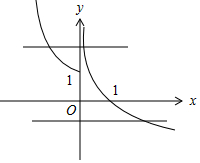
若关于x的方程f2(x)+f(x)+m=0有三个不同实数根,令f(x)=t,
则方程t2+t+m=0的两根一个大于等于1而另一个小于1.
再令g(t)=t2+t+m,则g(1)≤0,即2+m≤0,得m≤-2.
故选:B.
点评 本题考查的是方程的根的存在性以及根的个数判断,考查转化的思想、数形结合的思想方法,属中档题.

练习册系列答案
相关题目
20.若函数f(x)=aex-x-2a有两个零点,则实数a的取值范围是( )
| A. | $({-∞,\frac{1}{e}})$ | B. | $({0,\frac{1}{e}})$ | C. | (-∞,0) | D. | (0,+∞) |
7.若过点M(1,1)的直线l与圆(x-2)2+y2=4相较于两点A,B,且M为弦的中点AB,则|AB|为( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | $\sqrt{2}$ | D. | 2 |
17.下列说法正确的是( )
| A. | 若$\frac{1}{a}>\frac{1}{b}$,则a<b | |
| B. | 若命题$P:?x∈({0,π}),x+\frac{1}{sinx}≤2$,则?P为真命题 | |
| C. | 已知命题p,q,“p为真命题”是“p∧q为真命题”的充要条件 | |
| D. | 若f(x)为R上的偶函数,则$\int_{-1}^1{f(x)dx}=0$ |
1.向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 0 | D. | $-\frac{{\sqrt{3}}}{2}$ |