题目内容
函数f（x）=log5（x2-2x-3）的单调增区间是 ．
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=x2-2x-3＞0，求得函数的定义域，本题即求函数t=（x-1）2-4在定义域内的增区间．再利用二次函数的性质可得函数t=（x-1）2-4在定义域内的增区间．
解答：
解：令t=x2-2x-3＞0，求得x＜-1，或 x＞3，故函数的定义域为{x|x＜-1，或 x＞3}，
且f（x）=log5t，
本题即求函数t=（x-1）2-4在定义域内的增区间．
再利用二次函数的性质可得函数t=（x-1）2-4在定义域内的增区间为（3，+∞），
故答案为：（3，+∞）．
且f（x）=log5t，
本题即求函数t=（x-1）2-4在定义域内的增区间．
再利用二次函数的性质可得函数t=（x-1）2-4在定义域内的增区间为（3，+∞），
故答案为：（3，+∞）．
点评：本题主要考查复合函数的单调性，二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
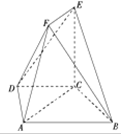如图所示的几何体，四边形ABCD中，有AB∥CD，∠BAC=30°，AB=2CD=2，CB=1．点E在平面ABCD内的射影是点C，EF∥AC，且AC=2EF．