题目内容
椭圆以x轴和y轴为对称轴,经过点(2,0),长轴长是短轴长的2倍,则椭圆的方程为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:椭圆的简单性质
专题:计算题,分类讨论,圆锥曲线的定义、性质与方程
分析:运用椭圆的性质,得a=2b,再讨论焦点的位置,即可得到a,b的值,进而得到椭圆方程.
解答:
解:由于椭圆长轴长是短轴长的2倍,
即有a=2b,
由于椭圆经过点(2,0),
则若焦点在x轴上,则a=2,b=1,
椭圆方程为
+y2=1;
若焦点y轴上,则b=2,a=4,
椭圆方程为
+
=1.
故选C.
即有a=2b,
由于椭圆经过点(2,0),
则若焦点在x轴上,则a=2,b=1,
椭圆方程为
| x2 |
| 4 |
若焦点y轴上,则b=2,a=4,
椭圆方程为
| y2 |
| 16 |
| x2 |
| 4 |
故选C.
点评:本题考查椭圆的方程和性质,注意讨论焦点位置,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)( )
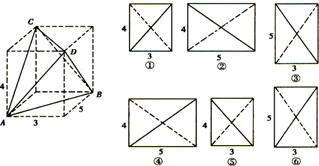

| A、①②⑥ | B、①②③ |
| C、④⑤⑥ | D、③④⑤ |