题目内容
已知函数f（x）=sinx+cosx，则f′（
）等于 ．
| π |
| 3 |
考点：导数的运算
专题：导数的综合应用
分析：利用导数的运算法则即可得出．
解答：
解：f′（x）=cosx-sinx，
∴f′（
）=cos
-sin
=
．
故答案为：
．
∴f′（
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
1-
| ||
| 2 |
故答案为：
1-
| ||
| 2 |
点评：本题考查了对数的运算法则，属于基础题．
练习册系列答案
相关题目
若在边长为1的正三角形ABC的边BC上有n（n∈N*，n≥2）等分点，沿向量
的方向依次为P1，P2，…，Pn，记Tn=
•
+
•
+…+
•
，若给出四个数值：①
②
③
④
，则Tn的值不可能共有（ ）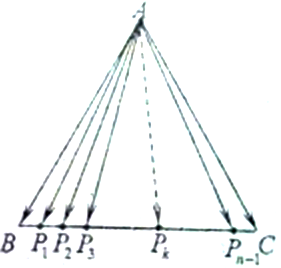
| BC |
| AB |
| AP1 |
| AP1 |
| AP2 |
| APn-1 |
| AC |
| 29 |
| 4 |
| 91 |
| 10 |
| 197 |
| 18 |
| 232 |
| 33 |
| A、1个 | B、2个 | C、3个 | D、4个 |
椭圆以x轴和y轴为对称轴，经过点（2，0），长轴长是短轴长的2倍，则椭圆的方程为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|