题目内容
已知函数f(x)=x|2a-x|+2x,a∈R.
(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;
(2)若函数f(x)在R上是增函数,求实数a的取值范围.
(3)求y=f(x)在区间[1,2]上的最大值.
(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;
(2)若函数f(x)在R上是增函数,求实数a的取值范围.
(3)求y=f(x)在区间[1,2]上的最大值.
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:(1)若a=0,根据函数奇偶性的定义即可判断函数y=f(x)的奇偶性;
(2)根据函数单调性的定义和性质,利用二次函数的性质即可求实数a的取值范围;
(3)根据a和区间的关系,建立条件关系即可得到结论.
(2)根据函数单调性的定义和性质,利用二次函数的性质即可求实数a的取值范围;
(3)根据a和区间的关系,建立条件关系即可得到结论.
解答:
解:(1)函数y=f(x)为奇函数.
当a=0时,f(x)=x|x|+2x,
∴f(-x)=-x|x|-2x=-f(x),
∴函数y=f(x)为奇函数;
(2)f(x)=
,
当x≥2a时,f(x)的对称轴为:x=a-1;
当x<2a时,y=f(x)的对称轴为:x=a+1;
∴当a-1≤2a≤a+1时,f(x)在R上是增函数,
即-1≤a≤1时,函数f(x)在R上是增函数;
(3)①当-1≤a≤1时,函数f(x)在R上是增函数,此时函数y=f(x)在区间[1,2]上的最大值为f(2)=4+2|4a-2|.
②当a>1时,即2a>a+1>a-1,
f(x)在(-∞,a+1)上单调增,在(a+1,2a)上单调减,在(2a,+∞)上单调增,此时函数y=f(x)在区间[1,2]上的最大值为f(2)=4+2|4a-2|
③当a<-1时,即2a<a-1<a+1,
f(x)在(-∞,2a)上单调增,在(2a,a-1)上单调减,在(a-1,+∞)上单调增,
此时函数y=f(x)在区间[1,2]上的最大值为f(2)=4+2|4a-2|.
当a=0时,f(x)=x|x|+2x,
∴f(-x)=-x|x|-2x=-f(x),
∴函数y=f(x)为奇函数;
(2)f(x)=
|
当x≥2a时,f(x)的对称轴为:x=a-1;
当x<2a时,y=f(x)的对称轴为:x=a+1;
∴当a-1≤2a≤a+1时,f(x)在R上是增函数,
即-1≤a≤1时,函数f(x)在R上是增函数;
(3)①当-1≤a≤1时,函数f(x)在R上是增函数,此时函数y=f(x)在区间[1,2]上的最大值为f(2)=4+2|4a-2|.
②当a>1时,即2a>a+1>a-1,
f(x)在(-∞,a+1)上单调增,在(a+1,2a)上单调减,在(2a,+∞)上单调增,此时函数y=f(x)在区间[1,2]上的最大值为f(2)=4+2|4a-2|
③当a<-1时,即2a<a-1<a+1,
f(x)在(-∞,2a)上单调增,在(2a,a-1)上单调减,在(a-1,+∞)上单调增,
此时函数y=f(x)在区间[1,2]上的最大值为f(2)=4+2|4a-2|.
点评:本题主要考查函数奇偶性和单调性的应用,根据分段函数的性质是解决本题的关键.综合性较强.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若在边长为1的正三角形ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量
的方向依次为P1,P2,…,Pn,记Tn=
•
+
•
+…+
•
,若给出四个数值:①
②
③
④
,则Tn的值不可能共有( )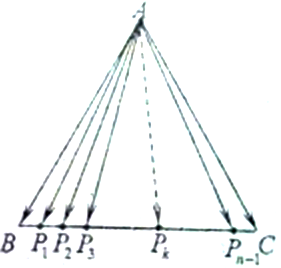
| BC |
| AB |
| AP1 |
| AP1 |
| AP2 |
| APn-1 |
| AC |
| 29 |
| 4 |
| 91 |
| 10 |
| 197 |
| 18 |
| 232 |
| 33 |

| A、1个 | B、2个 | C、3个 | D、4个 |
已知△ABC的外接圆半径为1,圆心为O,且3
+4
+5
=
,则
•
的值为( )
| OA |
| OB |
| OC |
| 0 |
| OC |
| AB |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
椭圆以x轴和y轴为对称轴,经过点(2,0),长轴长是短轴长的2倍,则椭圆的方程为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
