题目内容
11.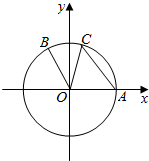 如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.
如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.(Ⅰ)求cos∠AOB;
(Ⅱ)求AC2.
分析 (Ⅰ)由条件任意角的三角函数的定义求得cos∠AOB 的值.
(Ⅱ)由条件利用同角三角函数的基本关系求出sin∠AOB 的值,再利用两角和差的余弦公式求得cos∠AOC=cos(∠AOB-∠AOC)的值,再利用余弦定理求得AC2 的值.
解答 解:(Ⅰ)由题意可得圆O的半径为OB=$\sqrt{5}$,∴cos∠AOB=$\frac{-1}{\sqrt{5}}$=-$\frac{\sqrt{5}}{5}$.
(Ⅱ)由以上可得,sin∠AOB=$\sqrt{{1-cos}^{2}∠AOB}$=$\frac{2\sqrt{5}}{5}$,又∠BOC=$\frac{π}{4}$,
∴cos∠AOC=cos(∠AOB-∠AOC)=cos∠AOB•cos∠BOC+sin∠AOB•sin∠BOC=-$\frac{\sqrt{5}}{5}$•$\frac{\sqrt{2}}{2}$+$\frac{2\sqrt{5}}{5}$•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{10}}{10}$,
∴AC2 =OA2+OC2-2OA•OC•cos∠AOC=5+5-10•$\frac{\sqrt{10}}{10}$=10-$\sqrt{10}$.
点评 本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,两角和的差的余弦公式,余弦定理,属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
6.已知集合A={(x,y)|$\sqrt{\frac{{x}^{2}}{9}}+\sqrt{\frac{{y}^{2}}{4}}≤1$},B={(x,y)|x-2y≤0},区域M=A∩B,则区域M的面积为( )
| A. | 6 | B. | 8 | C. | 12 | D. | 24 |
16.甲、乙两人各自独立随机地从区间[0,1]任取一数,分别记为x、y,则x2+y2>1的概率P=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1$-\frac{π}{4}$ |
20.已知△ABC的边BC上一动点D满足$\overrightarrow{CD}$=n$\overrightarrow{DB}$(n∈N*),$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则数列{(n+1)x}的前n项和为( )
| A. | $\frac{1}{n+1}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{2}n(n+1)$ | D. | $\frac{1}{2}(n+1)(n+2)$ |
1.某班有50人,从中选10人均分2组(即每组5人),一组打扫教室,一组打扫操场,那么不同的选派法有( )
| A. | $C_{50}^{10}•C_{10}^5$ | B. | $\frac{{C_{50}^{10}•C_{10}^5}}{2}$ | ||
| C. | $C_{50}^{10}•C_{10}^5•A_2^2$ | D. | $C_{50}^5•C_{45}^5•A_2^2$ |
 设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.
设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.