题目内容
9.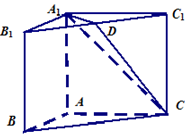 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题:
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题:(Ⅰ)求证:异面直线A1D与BC互相垂直;
(Ⅱ)求二面角(钝角)D-A1C-A的余弦值.
分析 (Ⅰ)AB,AC,AA1两两互相垂直,建立直角坐标系A-xyz,设AB=1,求出相关点的坐标,通过证明$\overrightarrow{{A}_{1}D}•\overrightarrow{BC}$=0,即可证明异面直线A1D与BC互相垂直.
(Ⅱ)求出平面DA1C的法向量,平面ACC1A1的法向量利用空间向量的数量积求解即可.
解答 解:因为侧面ABB1A1C1,ACC1A1均为正方形,∠BAC=90°,
所以AB,AC,AA1两两互相垂直,如图所示建立直角坐标系A-xyz…1分
设AB=1,则C(0,1,0),B(1,0,0),A1(0,0,1),D($\frac{1}{2}$,$\frac{1}{2}$,1).…3分
(Ⅰ)证明:由上可知:$\overrightarrow{{A_1}D}=({\frac{1}{2},\frac{1}{2},0})$,$\overrightarrow{BC}=({-1,1,0})$,…5分
所以$\overrightarrow{{A_1}D}•\overrightarrow{BC}=({-1,1,0})•({\frac{1}{2},\frac{1}{2},0})=-\frac{1}{2}+\frac{1}{2}+0=0$,…6分
所以$\overrightarrow{{A_1}D}⊥\overrightarrow{BC}$,
所以,异面直线A1D与BC互相垂直.…7分
(Ⅱ)解:$\overrightarrow{{A}_{1}D}$=($\frac{1}{2}$,$\frac{1}{2}$,0),$\overrightarrow{{A}_{1}C}$=(0,1,-1),…9分
设平面DA1C的法向量为$\overrightarrow{n}$=(x,y,z),则有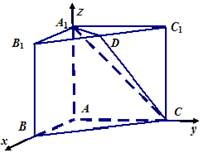
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}D}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}C}=0}\end{array}\right.$,$\left\{\begin{array}{l}{x+y=0}\\{y-z=0}\end{array}\right.$,
取x=1,得$\overrightarrow{n}$=(1,-1,-1)…10分
又因为AB⊥平面ACC1A1,所以平面ACC1A1的法向量为$\overrightarrow{AB}$=(1,0,0),…11分
∴cos$<\overrightarrow{n},\overrightarrow{AB}>$=$|\frac{\overrightarrow{n}•\overrightarrow{AB}}{|\overrightarrow{n}||\overrightarrow{AB}|}|$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
因为二面角D-A1C-A是钝角,
所以,二面角D-A1C-A的余弦值为$-\frac{{\sqrt{3}}}{3}$.…12分.
点评 本题考查二面角的平面角的求法,直线与直线所成角的求法,考查空间向量的应用,转化思想的应用.

| A. | $\frac{\sqrt{6π}}{6}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{2π}}{2}$ | D. | $\frac{3\sqrt{π}}{2π}$ |
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
| A. | -$\overrightarrow{a}$+3$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-3$\overrightarrow{b}$ | C. | 3$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | -3$\overrightarrow{a}$+$\overrightarrow{b}$ |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 点 | B. | 线段 | C. | 正方形 | D. | 圆 |