题目内容
14.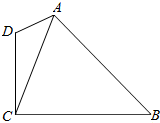 如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$
如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$(Ⅰ)求△ACD的面积;
(Ⅱ)若∠ACB=60°,求AB的长.
分析 (Ⅰ)由题意和二倍角公式可得cosD,进而可得sinD,代入面积公式S=$\frac{1}{2}$•AD•CD•sinD,计算可得;
(II)在△ACD中,由余弦定理可得AC,进而在△ABC中由正弦定理可得AB.
解答 解:(Ⅰ)∵∠D=2∠B,∴cosD=2cos2B-1=2×($\frac{\sqrt{6}}{4}$)2-1=-$\frac{1}{4}$,
∵∠D∈(0,π),∴sinD=$\sqrt{1-co{s}^{2}D}$=$\frac{\sqrt{15}}{4}$,
∵AD=2,CD=3,∴△ACD的面积S=$\frac{1}{2}$•AD•CD•sinD=$\frac{3}{4}$$\sqrt{15}$;
(II)在△ACD中,由余弦定理可得AC=$\sqrt{A{D}^{2}+C{D}^{2}-2AD•CD•cosD}$
=$\sqrt{9+4-2×3×2×(-\frac{1}{4})}$=4
在△ABC中,由正弦定理可得$\frac{AC}{sinB}$=$\frac{AB}{sin∠ACB}$,
∴AB=$\frac{4×\frac{\sqrt{3}}{2}}{\frac{\sqrt{10}}{4}}$=$\frac{4\sqrt{30}}{5}$.
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属中档题.

练习册系列答案
相关题目
5.已知点A(0,1),B(3,2),C(a,0),若A,B,C三点共线,则a=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | -2 | D. | -3 |
9.在△ABC中,若A=30°,a=2,b=2$\sqrt{3}$,则此三角形解的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 不能确定 |
19.直线y=k(x-1)+2与抛物线x2=4y的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |