题目内容
19.直线y=k(x-1)+2与抛物线x2=4y的位置关系为( )| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
分析 直线y=k(x-1)+2过定点(1,2),在抛物线x2=4y内部,即可得出结论.
解答 解:直线y=k(x-1)+2过定点(1,2),
∵12<4×2,
∴(1,2)在抛物线x2=4y内部,
∴直线y=k(x-1)+2与抛物线x2=4y相交,
故选:A.
点评 本题考查直线与抛物线的位置关系,确定直线过定点是关键.

练习册系列答案
相关题目
9.已知抛物线x2=2py(p>0),斜率为1的直线交抛物线于A,B两点,若线段AB中点的横坐标为2,则该抛物线的准线方程为( )
| A. | y=-1 | B. | y=1 | C. | y=-2 | D. | y=2 |
7.两座灯塔A和B与海岸观察站C的距离都等于a海里,灯塔A在观测站C北偏东75°的方向上,灯塔B在观测站C的东南方向,则灯搭A和B之间的距离为( )
| A. | a海里 | B. | $\sqrt{2}$a海里 | C. | $\sqrt{3}$a海里 | D. | 2a海里 |
4.在等腰直角三角形ABC中,AB=AC=1,点E为斜边BC的中点,点M在线段AB上运动,则($\overline{AE}$-$\overline{AM}$)•($\overline{AC}$-$\overline{AM}$)的取值范围是( )
| A. | [$\frac{7}{16}$,$\frac{1}{2}$] | B. | [$\frac{7}{16}$,1] | C. | [$\frac{1}{2}$,1] | D. | [0,1] |
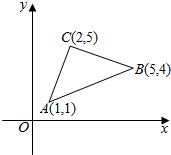 如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.
如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.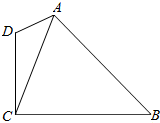 如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$
如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$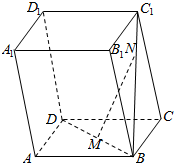 如图所示,已知几何体ABCD-A1B1C1D1是平行六面体.
如图所示,已知几何体ABCD-A1B1C1D1是平行六面体.