题目内容
9.在△ABC中,若A=30°,a=2,b=2$\sqrt{3}$,则此三角形解的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 不能确定 |
分析 计算bsinA的值,比较其和a、b的大小关系可得.
解答 解:∵在△ABC中A=30°,a=2,b=2$\sqrt{3}$,
∴bsinA=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,
而$\sqrt{3}$<a=2<b=2$\sqrt{3}$,
∴三角形解的个数为2,
故选:C.
点评 本题考查三角形解得个数的判断,属基础题.

练习册系列答案
相关题目
19.“方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线”是“n>-1”的( )
| A. | 充分不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知正项等比数列{an},其前n项和为Sn,ak-1=2,ak•ak+2=a${\;}_{5}^{2}$=64,则S10等于( )
| A. | 410-1 | B. | $\frac{{4}^{10}-1}{3}$ | C. | 210-1 | D. | $\frac{{2}^{10}-1}{2}$ |
4.已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,点P($\frac{1}{2}$,m)是抛物线C上一点,若点P到直线l的距离等于点P到坐标原点O的距离,则点F到准线l的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.幂函数的图象过点(5,$\sqrt{5}$),则它的单调递增区间是( )
| A. | [0,+∞) | B. | [-1,+∞) | C. | (-∞,+∞) | D. | (-∞,0) |
19.已知变量x,y之间具有线性相关关系,其散点图如图所示,则其回归方程可能为( )
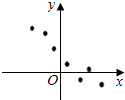

| A. | $\widehat{y}$=1.5x+2 | B. | $\widehat{y}$=-1.5x+2 | C. | $\widehat{y}$=1.5x-2 | D. | $\widehat{y}$=-1.5x-2 |
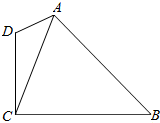 如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$
如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$