题目内容

4．已知f（x）=ax2-（a+2）x+2．
（1）若实数a＜0，求关于x的不等式f（x）＞0的解集；
（2）若“$\frac{1}{2}$≤x≤$\frac{3}{4}$”是“f（x）+2x＜0”的充分条件，求正实数a的取值范围．

分析 （1）f（x）=ax2-（a+2）x+2=（ax-2）（x-1），a＜0，可得ax2-（a+2）x+2=0的两根为$\frac{2}{a}$，且$\frac{2}{a}$＜1，即可得出．
（2）f（x）+2x＜0化为：g（x）=ax2-ax+2＜0，由“$\frac{1}{2}$≤x≤$\frac{3}{4}$”是“f（x）+2x＜0”的充分条件，可得$\left\{\begin{array}{l}{g（\frac{1}{2}）＜0}\\{g（\frac{3}{4}）＜0}\end{array}\right.$，又a＞0，解得a范围．

解答 解：（1）f（x）=ax2-（a+2）x+2=（ax-2）（x-1），∵a＜0，∴ax2-（a+2）x+2=0的两根为$\frac{2}{a}$，且$\frac{2}{a}$＜1．
∴关于x的不等式f（x）＞0的解集为$（\frac{2}{a}，1）$．
（2）f（x）+2x＜0化为：g（x）=ax2-ax+2＜0，
∵“$\frac{1}{2}$≤x≤$\frac{3}{4}$”是“f（x）+2x＜0”的充分条件，
∴$\left\{\begin{array}{l}{g（\frac{1}{2}）＜0}\\{g（\frac{3}{4}）＜0}\end{array}\right.$，又a＞0，解得a＞$\frac{32}{3}$．
∴正实数a的取值范围是$（\frac{32}{3}，+∞）$．

点评 本题考查了一元二次不等式与一元二次方程的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
14．已知函数y=sin（ωx+$\frac{π}{3}$）向右平移$\frac{π}{3}$个单位后，所得的图象与原函数图象关于x轴对称，则ω的最小正值为（　　）
A．1B．2C．$\frac{5}{2}$D．3
15．函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，x≥0}\\{g（x）+a，x＜0}\end{array}\right.$为奇函数，若g（-2）=4，则a=（　　）
A．-3B．4C．-7D．6
12．若函数f（x）=x2+ax+$\frac{1}{x}$在[$\frac{1}{3}$，+∞）上是增函数，则实数a的取值范围是（　　）
A．[-1，0]B．[0，$\frac{25}{3}$]C．[$\frac{25}{3}$，+∞）D．[9，+∞）
19．“方程$\frac{{x}^{2}}{2+n}$-$\frac{{y}^{2}}{n+1}$=1表示双曲线”是“n＞-1”的（　　）
A．充分不必要条件B．必要且不充分条件
C．充要条件D．既不充分也不必要条件
9．已知抛物线x2=2py（p＞0），斜率为1的直线交抛物线于A，B两点，若线段AB中点的横坐标为2，则该抛物线的准线方程为（　　）
A．y=-1B．y=1C．y=-2D．y=2
16．已知a，b是两条不重合的直线，α，β是两个不同的平面，则下列命题中正确的是（　　）
A．若a⊥b，a⊥α，则b∥αB．若a⊥α，b∥α，则a⊥b
C．若a∥b，b?α，则a∥αD．若a，b?α，a∥β，b∥β，则α∥β
13．若函数f（x）的定义域为D，任取x1、x2∈D，都有|f（x1）-f（x2）|≤|x1-x2|成立，则称f（x）为D上的“收缩”函数．）
（1）判断f（x）=$\frac{1}{4}$x2+$\frac{1}{2}$x在[-1，1]上是否为“收缩”函数，并说明理由；
（2）是否存在k∈R，使f（x）=k$\sqrt{{x}^{2}+1}$在R上位“收缩“函数，若存在，求k的取值范围，若不存在，说明理由；
（3）若D=[0，1]，f（0）=f（1），且f（x）为”收缩“函数，?x1、x2∈D，|f（x1）-f（x2）|≤$\frac{1}{2}$能否恒成立并说明理由？
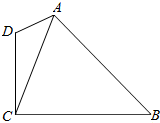14．如图所示，在四边形ABCD中，AD=2，CD=3，∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$
（Ⅰ）求△ACD的面积；
（Ⅱ）若∠ACB=60°，求AB的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网