题目内容
2.某人上午7时,乘摩托艇从A港出发前往B港,所需时间x至少为3小时,至多为10小时,然后从B港乘汽车前往C市,所需时间y至少为2.5小时,至多为12.5小时,且要求到达C市的时间为同一天下午4时至9时之间,若从A港到C市所需要的经费ω=100+3(5-x)+2(8-y)元,则所需经费的最小值为93(元)分析 通过3≤x≤10、2.5≤y≤12.5、9≤x+y≤14,得出目标函数3x+2y=31-ω,进而结合简单线性规划,计算即得结论.
解答 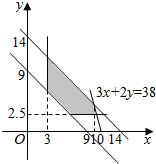 解:依题意,3≤x≤10,2.5≤y≤12.5,
解:依题意,3≤x≤10,2.5≤y≤12.5,
则9≤x+y≤14,
∵ω═3(5-x)+2(8-y),
∴3x+2y=31-ω,
设31-ω=k,则当k最大时ω最小,
如图,通过阴影部分区域且斜率为-$\frac{3}{2}$的直线3x+2y=k中,使k值最大的直线必经过点(10,4),
即当y=4时ω最小,
此时ω最小值为131-(30+8)=93元,
故答案为:93.
点评 本题考查函数的最值及其几何意义,考查分析问题、解决问题的能力,涉及线性规划等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
12.若函数f(x)=x2+ax+$\frac{1}{x}$在[$\frac{1}{3}$,+∞)上是增函数,则实数a的取值范围是( )
| A. | [-1,0] | B. | [0,$\frac{25}{3}$] | C. | [$\frac{25}{3}$,+∞) | D. | [9,+∞) |
17.已知正项等比数列{an},其前n项和为Sn,ak-1=2,ak•ak+2=a${\;}_{5}^{2}$=64,则S10等于( )
| A. | 410-1 | B. | $\frac{{4}^{10}-1}{3}$ | C. | 210-1 | D. | $\frac{{2}^{10}-1}{2}$ |
7.两座灯塔A和B与海岸观察站C的距离都等于a海里,灯塔A在观测站C北偏东75°的方向上,灯塔B在观测站C的东南方向,则灯搭A和B之间的距离为( )
| A. | a海里 | B. | $\sqrt{2}$a海里 | C. | $\sqrt{3}$a海里 | D. | 2a海里 |
12.已知数列{an}满足log3an+2=log3an+1(n∈N*)且a2+a4+a6=9,则log${\;}_{\frac{1}{3}}$(a5+a7+a9)的值是( )
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{8}$ |
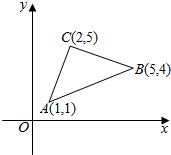 如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.
如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.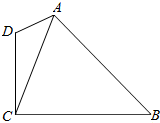 如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$
如图所示,在四边形ABCD中,AD=2,CD=3,∠D=2∠B且cosB=$\frac{\sqrt{6}}{4}$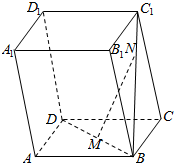 如图所示,已知几何体ABCD-A1B1C1D1是平行六面体.
如图所示,已知几何体ABCD-A1B1C1D1是平行六面体.