题目内容
求下列函数的值域:
(1)f(x)=2x2-3x-1;
(2)f(x)=
;
(3)f(x)=x+
;
(4)f(x)=2x-
;
(5)f(x)=
;
(6)f(x)=5-x+
.
(1)f(x)=2x2-3x-1;
(2)f(x)=
| x2+2x |
| x2-x |
(3)f(x)=x+
| x+1 |
(4)f(x)=2x-
| x+2 |
(5)f(x)=
| x2-1 |
| x2+1 |
(6)f(x)=5-x+
| 3x-1 |
考点:函数的值域
专题:函数的性质及应用
分析:(1)由二次函数的图象与性质,先求出函数的最值,即得出值域;
(2)分离常数,利用二次函数的判别式求出值域;
(3)配方法,配成以
为自变量的二次函数,从而求出函数的值域;
(4)配方法,配成以
为自变量的二次函数,从而求出函数的值域;
(5)分离常数法,把函数f(x)化为1-
,求出
的范围即得f(x)的值域;
(6)换元法,设t=
,求二次函数在闭区间上的最值即得值域.
(2)分离常数,利用二次函数的判别式求出值域;
(3)配方法,配成以
| x+1 |
(4)配方法,配成以
| x+2 |
(5)分离常数法,把函数f(x)化为1-
| 2 |
| x2+1 |
| 2 |
| x2+1 |
(6)换元法,设t=
| 3x-1 |
解答:
解:(1)∵f(x)=2x2-3x-1是二次函数,图象是抛物线,且开口向上,
∴f(x)有最小值是
=-
,
∴f(x)的值域是[-
,+∞);
(2)∵y=f(x)=
=
=1+
,
∵x≠0,∴y≠1;
∴(y-1)(x2-x)=3x,
即(y-1)x2-(y+2)x=0,
判别式[-(y+2)]2≥0恒成立,
∴函数f(x)的值域是{y|y≠1};
(3)∵f(x)=x+
=x+1+
-1
=(
+
)2-
≥
-
=-1,
∴f(x)的值域是[-1,+∞);
(4)∵f(x)=2x-
=2(x+2)-4-
=2(
-
)2-4-
≥2×0-
=-
,
∴f(x)的值域是[-
,+∞);
(5)∵f(x)=
=
=1-
,
又x2+1≥1,
∴0<
≤2,
∴-1≤1-
<1,
∴f(x)的值域是[-1,1);
(6)令t=
,且t≥0;
∴x=
(t2+1),
∴y=5-
(t2+1)+t
=-
t2+t+
=-
(t-
)2+
+
≤-
×0+
=
,
∴f(x)的值域是(-∞,
].
∴f(x)有最小值是
| 4×2×(-1)-(-3)2 |
| 4×2 |
| 17 |
| 8 |
∴f(x)的值域是[-
| 17 |
| 8 |
(2)∵y=f(x)=
| x2+2x |
| x2-x |
| x2-x+3x |
| x2-x |
| 3x |
| x2-x |
∵x≠0,∴y≠1;
∴(y-1)(x2-x)=3x,
即(y-1)x2-(y+2)x=0,
判别式[-(y+2)]2≥0恒成立,
∴函数f(x)的值域是{y|y≠1};
(3)∵f(x)=x+
| x+1 |
=x+1+
| x+1 |
=(
| x+1 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
=-1,
∴f(x)的值域是[-1,+∞);
(4)∵f(x)=2x-
| x+2 |
=2(x+2)-4-
| x+2 |
=2(
| x+2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 33 |
| 8 |
=-
| 33 |
| 8 |
∴f(x)的值域是[-
| 33 |
| 8 |
(5)∵f(x)=
| x2-1 |
| x2+1 |
=
| x2+1-2 |
| x2+1 |
=1-
| 2 |
| x2+1 |
又x2+1≥1,
∴0<
| 2 |
| x2+1 |
∴-1≤1-
| 2 |
| x2+1 |
∴f(x)的值域是[-1,1);
(6)令t=
| 3x-1 |
∴x=
| 1 |
| 3 |
∴y=5-
| 1 |
| 3 |
=-
| 1 |
| 3 |
| 14 |
| 3 |
=-
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 4 |
| 14 |
| 3 |
| 1 |
| 3 |
| 65 |
| 12 |
=
| 65 |
| 12 |
∴f(x)的值域是(-∞,
| 65 |
| 12 |
点评:本题考查了求函数值域的常用方法,即函数的最值法、配方法、换元法、分离常数法等,是综合题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设变量x,y满足
,则目标函数z=3x-y的最小值为( )
|
| A、1 | B、2 | C、3 | D、4 |
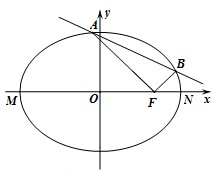 已知椭圆
已知椭圆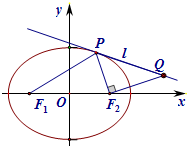 在平面直角坐标系xoy中,已知F1,F2分别是椭圆G:
在平面直角坐标系xoy中,已知F1,F2分别是椭圆G: