题目内容
 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,
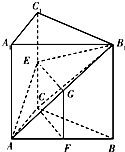
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB的中点,AC=BC=1,AA1=2.
(Ⅰ)求证:CF∥平面AB1E;
(Ⅱ)求三棱锥C-AB1E在底面AB1E上的高.
考点:直线与平面平行的判定,棱柱的结构特征,棱锥的结构特征
专题:空间位置关系与距离
分析:(Ⅰ)取AB1的中点G,连接EG,FG,由已知得四边形FGEC是平行四边形,由此能证明CF∥平面AB1E.
(Ⅱ)由已知得BB1⊥平面ABC,AC⊥BB1,AC⊥BC,从而AC⊥平面EB1C,进而AC⊥B1C,由此利用VC-AB1E=VA-EB1C,能求出三棱锥C-AB1E在底面AB1E上的高.
(Ⅱ)由已知得BB1⊥平面ABC,AC⊥BB1,AC⊥BC,从而AC⊥平面EB1C,进而AC⊥B1C,由此利用VC-AB1E=VA-EB1C,能求出三棱锥C-AB1E在底面AB1E上的高.
解答:
(Ⅰ)证明:取AB1的中点G,连接EG,FG,
因为F,G分别是AB,AB1的中点,
所以FG∥BB1,FG=
BB1,
因为E为侧棱CC1的中点,所以FG∥EC,FG=EC,…(3分)
所以四边形FGEC是平行四边形,则CF∥EG,
因为CF?平面AB1E,EG?平面AB1E,
所以CF∥平面AB1E.…(6分)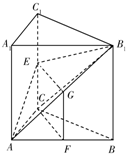
(Ⅱ)解:因为三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,
所以BB1⊥平面ABC,
又AC?平面ABC,所以AC⊥BB1,
又∠ACB=90°,所以AC⊥BC,
因为BB1∩BC=B,
所以AC⊥平面EB1C,所以AC⊥B1C,
得VA-EB1C=
S△EB1C•AC=
×(
×1×1)×1=
,…(10分)
因为AE=EB1=
,AB1=
,
所以S△AB1E=
,
因为VC-AB1E=VA-EB1C,
所以三棱锥C-AB1E在底面AB1E上的高为
=
.…(12分)
因为F,G分别是AB,AB1的中点,
所以FG∥BB1,FG=
| 1 |
| 2 |
因为E为侧棱CC1的中点,所以FG∥EC,FG=EC,…(3分)
所以四边形FGEC是平行四边形,则CF∥EG,
因为CF?平面AB1E,EG?平面AB1E,
所以CF∥平面AB1E.…(6分)

(Ⅱ)解:因为三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,
所以BB1⊥平面ABC,
又AC?平面ABC,所以AC⊥BB1,
又∠ACB=90°,所以AC⊥BC,
因为BB1∩BC=B,
所以AC⊥平面EB1C,所以AC⊥B1C,
得VA-EB1C=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
因为AE=EB1=
| 2 |
| 6 |
所以S△AB1E=
| ||
| 2 |
因为VC-AB1E=VA-EB1C,
所以三棱锥C-AB1E在底面AB1E上的高为
| 3VC-AB1E |
| S△AB1E |
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查三棱锥的高的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
下列求导函数运算正确的是( )
A、(x+
| ||||
B、(
| ||||
| C、[(3+x2)(2-x3)]′=2x(2-x3)-3x2(3+x2) | ||||
| D、(x2•cosx)′=2x•cosx+x2•sinx |
若A(x1,y1)、B(x2,y2)为平面直角坐标系xOy上的两点,定义由A点到B点的一种折线距离ρ(A,B)=|x2-x1|+|y2-y1|.已知点N(1,0),点M为直线3x+4y-5=0上的动点,则ρ(M,N)的最小值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC的内角A,B,C的对边分别为a,b,c,若a=10,B=45°,b=7,则△ABC( )
| A、无解 | B、仅有一解 |
| C、仅有两解 | D、无法判断 |
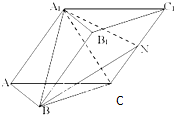 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,N是CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,N是CC1的中点.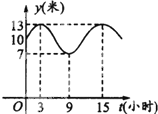 某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据: