题目内容
△ABC的内角A,B,C的对边分别为a,b,c,若a=10,B=45°,b=7,则△ABC( )
| A、无解 | B、仅有一解 |
| C、仅有两解 | D、无法判断 |
考点:正弦定理
专题:解三角形
分析:利用正弦定理列出关系式,把sinB,a,b的值代入求出sinA的值,确定出A解的个数即可做出判断.
解答:
解:∵△ABC中,a=10,B=45°,b=7,
∴由正弦定理
=
得:sinA=
=
=
>1,
则△ABC无解.
故选:A.
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
10×
| ||||
| 7 |
5
| ||
| 7 |
则△ABC无解.
故选:A.
点评:此题考查了正弦定理,以及正弦函数的性质,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
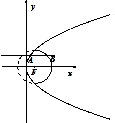 如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A、(6,8) |
| B、(4,6) |
| C、(8,12) |
| D、(8,10) |
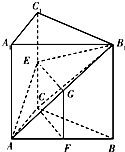 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,


