题目内容
在平面直角坐标系xoy中,M(x,y)为不等式组
所表示的区域上一动点,则z=
的最小值为( )
|
| y |
| x |
| A、2 | ||
| B、1 | ||
C、-
| ||
D、-
|
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,利用z的几何意义即可得到结论.
解答:
 解:作出线性区域如图:
解:作出线性区域如图:
z=
的几何意义是动点P(x,y)到原点的斜率,由图象可知OA的斜率最小,
由
,解得
,即A(3,-1),
则z=
的最小值为
=-
,
故选:D
 解:作出线性区域如图:
解:作出线性区域如图:z=
| y |
| x |
由
|
|
则z=
| y |
| x |
| -1 |
| 3 |
| 1 |
| 3 |
故选:D
点评:本题主要考查线性规划的应用,根据目标函数的几何意义结合斜率公式是解决本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 一个正方形被分成九个相等的小正方形,将中间的一个正方形挖去,如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间的一个挖去,得图(2);如此继续下去,则第n个图共挖去小正方形( )
一个正方形被分成九个相等的小正方形,将中间的一个正方形挖去,如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间的一个挖去,得图(2);如此继续下去,则第n个图共挖去小正方形( )| A、(8n-1)个 | ||
| B、(8n+1)个 | ||
C、
| ||
D、
|
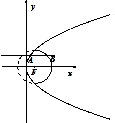 如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A、(6,8) |
| B、(4,6) |
| C、(8,12) |
| D、(8,10) |
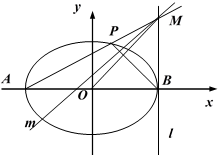 (1)求椭圆E的方程;
(1)求椭圆E的方程;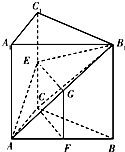 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,