题目内容
已知等差数列{an}的前n项和为Sn，且满足a2+a5=12，则S6=（ ）
| A、36 | B、35 | C、25 | D、24 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由等差数列的性质可得a1+a6=a2+a5=12，整体代入等差数列的求和公式可得．
解答：
解：由等差数列的性质可得a1+a6=a2+a5=12，
∴S6=
=
=36
故选：A
∴S6=
| 6(a1+a6) |
| 2 |
| 6×12 |
| 2 |
故选：A
点评：本题考查等差数列的性质和求和公式，属基础题．
练习册系列答案
相关题目
函数f1（x）=
，f2（x）=
，…，fn+1（x）=
，…，则函数f2015（x）是（ ）
| 1 |
| x |
| 1 |
| x+f1(x) |
| 1 |
| x+fn(x) |
| A、奇函数但不是偶函数 |
| B、偶函数但不是奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
若复数z=
，则|z|=（ ）
| 2 | ||
1+
|
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
等差数列{an}的前n项和为Sn，且S3=6，a3=0，则公差d等于（ ）
| A、-1 | B、1 | C、2 | D、-2 |
函数f（x）=log2（x+1）的定义域为（ ）
| A、（0，+∞） |
| B、[-1，+∞） |
| C、（-1，+∞） |
| D、（1，+∞） |
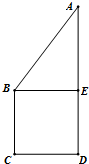如图正方形BCDE的边长为a，已知AB=