题目内容
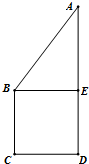 如图正方形BCDE的边长为a,已知AB=
如图正方形BCDE的边长为a,已知AB=| 3 |
①AB与DE所成角的正切值是
| 2 |
②AB∥CE;
③VB-ACE的体积是
| 1 |
| 6 |
④平面ABC⊥平面ADC;
⑤直线EA与平面ADB所成角为30°.
其中正确的有
考点:命题的真假判断与应用,空间中直线与直线之间的位置关系,平面与平面之间的位置关系
专题:空间位置关系与距离
分析:①由于BC∥DE,则∠ABC(或其补角)为AB与DE所成角;
②AB和CE是异面直线;
③根据三棱锥的体积公式即可求VB-ACE的体积;
④根据面面垂直的判定定理即可证明;
⑤根据直线和平面所成角的定义进行求解即可.
②AB和CE是异面直线;
③根据三棱锥的体积公式即可求VB-ACE的体积;
④根据面面垂直的判定定理即可证明;
⑤根据直线和平面所成角的定义进行求解即可.
解答:
解:由题意,AB=
BC,AE=
a,
AD⊥平面BCDE,AD=a,AC=
a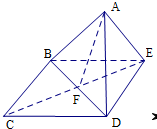
①由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角
∵AB=
a,BC=a,AC=
a,
∴BC⊥AC,∴tan∠ABC=
,故①正确;
②由图象可知AB与CE是异面直线,故②错误.
③VB-ACE的体积是
S△BCE×AD=
×
a3=
a3,故③正确;
(4)∵AD⊥平面BCDE,BC?平面BCDE,
∴AD⊥BC,∵BC⊥CD,AD∩CD=D,∴BC⊥平面ADC,
∵BC?平面ABC,∴平面ABC⊥平面ADC,故④正确;
⑤连接CE交BD于F,则EF⊥BD,
∵平面ABD⊥平面BDE,
∴EF⊥平面ABD,连接F,
则∠AFE为直线AE与平面ABD所成角,
在△AFE中,EF=
a,AE=
a,
∴sin∠EAF=
=
,则∠EAF=30°,故⑤正确,
故正确的是①③④⑤
故答案为:①③④⑤
| 3 |
| 2 |
AD⊥平面BCDE,AD=a,AC=
| 2 |

①由于BC∥DE,∴∠ABC(或其补角)为AB与DE所成角
∵AB=
| 3 |
| 2 |
∴BC⊥AC,∴tan∠ABC=
| 2 |
②由图象可知AB与CE是异面直线,故②错误.
③VB-ACE的体积是
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(4)∵AD⊥平面BCDE,BC?平面BCDE,
∴AD⊥BC,∵BC⊥CD,AD∩CD=D,∴BC⊥平面ADC,
∵BC?平面ABC,∴平面ABC⊥平面ADC,故④正确;
⑤连接CE交BD于F,则EF⊥BD,
∵平面ABD⊥平面BDE,
∴EF⊥平面ABD,连接F,
则∠AFE为直线AE与平面ABD所成角,
在△AFE中,EF=
| ||
| 2 |
| 2 |
∴sin∠EAF=
| EF |
| AF |
| 1 |
| 2 |
故正确的是①③④⑤
故答案为:①③④⑤
点评:本题考查图形的翻折,考查空间线面位置关系,搞清翻折前后的变与不变是关键.综合性较强,难度较大.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,且满足a2+a5=12,则S6=( )
| A、36 | B、35 | C、25 | D、24 |
已知函数f(x)=
-lnx,则有下列结论中错误的是( )
| lnx |
| 1+x |
| A、?x0∈R,f(x)=0 | ||
| B、若x0是f(x)的最大值点,则f(x0)=x0 | ||
C、若x0是f(x)的最大值点,则f(x0)<
| ||
| D、若x0是f(x)的极大值点,则f(x)在(x0,+∞)上单调递增 |
已知点P(3,m)在直线x+y-1=0上,则m的值为( )
| A、5 | B、2 | C、-2 | D、-6 |
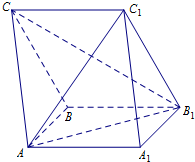 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C. 如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0),且双曲线经过点P(2,3).
如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0),且双曲线经过点P(2,3).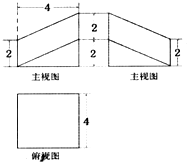 棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是