题目内容
3.在△ABC中,角A,B,C的对边分别为a,b,c,已知sinBsin($\frac{π}{4}$+A)-sinAsin($\frac{π}{4}$+B)=sin$\frac{π}{4}$.(1)求证:B-A=$\frac{π}{2}$;
(2)求sinA+sinC的取值范围.
分析 (1)根据三角函数的正弦的和差公式即可证明,
(2)sinA+sinC经过化简后得到-(sinA-$\frac{1}{2}$)2+$\frac{5}{4}$,根据0<sinA<1,得到取值范围.
解答 解:(1):sinBsin($\frac{π}{4}$+A)-sinAsin($\frac{π}{4}$+B),
=$\frac{\sqrt{2}}{2}$sinB(sinA+cosA)-$\frac{\sqrt{2}}{2}$sinA(sinB+cosB),
=$\frac{\sqrt{2}}{2}$(sinBsinA+sinBcosA-sinAsinB-sinAcosB),
=$\frac{\sqrt{2}}{2}$(sinBcosA-sinAcosB),
=$\frac{\sqrt{2}}{2}$sin(B-A)=sin$\frac{π}{4}$,
∴sin(B-A)=1,
∴B-A=$\frac{π}{2}$;
(2)sinA+sinC=sinA+sin(B+A)=sinA+sin($\frac{π}{2}$+2A)=sinA+cos2A=sinA+1-sin2A=-(sinA-$\frac{1}{2}$)2+$\frac{5}{4}$,
∵0<sinA<1,
∴1<-(sinA-$\frac{1}{2}$)2+$\frac{5}{4}$≤$\frac{5}{4}$,
∴sinA+sinC的取值范围为(1,$\frac{5}{4}$].
点评 本题考查了三角函数的化简以及三角函数的性质,属于中档题.

练习册系列答案
相关题目
13.若a,b∈R,且ab>0,则“a=b”是“$\frac{b}{a}+\frac{a}{b}≥2$等号成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |
12.下列函数中是奇函数,且最小正周期是π的函数是( )
| A. | y=tan2x | B. | y=sinx | C. | y=cos2x | D. | y=sin2x |
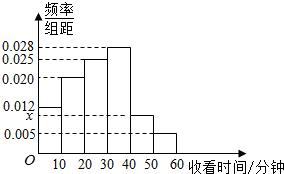 某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01.
某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].则图中x的值为0.01. 如图,x轴非负半轴平分∠AOB,∠AOx=α,动圆P截OA所得弦MN=2a,截OB所得弦SQ=2b,试求动圆圆心P的轨迹方程.
如图,x轴非负半轴平分∠AOB,∠AOx=α,动圆P截OA所得弦MN=2a,截OB所得弦SQ=2b,试求动圆圆心P的轨迹方程. 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2$\sqrt{5}$km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2$\sqrt{5}$km.现欲在此地块内建一形状为直角梯形DECF的科技园区.