题目内容
18. 如图,x轴非负半轴平分∠AOB,∠AOx=α,动圆P截OA所得弦MN=2a,截OB所得弦SQ=2b,试求动圆圆心P的轨迹方程.
如图,x轴非负半轴平分∠AOB,∠AOx=α,动圆P截OA所得弦MN=2a,截OB所得弦SQ=2b,试求动圆圆心P的轨迹方程.
分析 建立如图所示的坐标系,由题意∠AOB=2α,利用勾股定理,确定d12-d22=b2-r2,即可求动圆圆心P的轨迹方程.
解答 解:建立如图所示的坐标系,由题意∠AOB=2α,动圆在角两边OA,OB上截得弦长分别为|MN|=2a,|QS|=2b,
设P(x,y)为轨迹上任一点,设动圆半径为r,点P到OA,OB的距离分别为|PC|=d1,|PD|=d2,
∴d12+a2=d22+b2=r2,
∴d12-d22=b2-r2,①
直线OA,OB的方程分别为OA:xsinα-ycosα=0,OB:xsinα+ycosα=0
∴d1=|xsinα-ycosα|,d2=|xsinα+ycosα|
代入①化简可得2xysin2α=a2-b2.
点评 本题考查轨迹方程,考查直接法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.已知i是虚数单位,则复数i(1+i)的共轭复数为( )
| A. | 1+i | B. | l-i | C. | -l+i | D. | -l-i |
13.正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BB1,CD的中点,则点F到平面A1D1E的距离为( )
| A. | $\frac{3}{10}$a | B. | $\frac{3\sqrt{7}}{10}$a | C. | $\frac{3\sqrt{5}}{10}$a | D. | $\frac{7}{10}$a |
8.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥与外接球的体积比为( )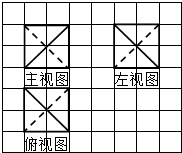

| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
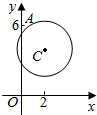 已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)
已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)