题目内容
14.已知数列{an},${a_n}∈{N^*}$,${S_n}=\frac{1}{8}{({a_n}+2)^2}$,求an=4n-2.分析 当n≥2时,利用an=Sn-Sn-1化简计算可知an-an-1=4,进而可知数列{an}是首项为2、公差为4的等差数列,计算即得结论.
解答 解:∵${S_n}=\frac{1}{8}{({a_n}+2)^2}$,
∴当n≥2时,an=Sn-Sn-1=$\frac{1}{8}$[$({a}_{n}+2)^{2}$-$({a}_{n-1}+2)^{2}$],
整理得:an-an-1=4,
又∵a1=$\frac{1}{8}$$({{a}_{1}+2)}^{2}$,
∴a1=2,
∴数列{an}是首项为2、公差为4的等差数列,
∴an=4n-2,
故答案为:4n-2.
点评 本题考查数列的通项,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
5.已知函数f(x)=ex+3,则f(x)在x=0处切线的方程是( )
| A. | x-y+4=0 | B. | x+y-4=0 | C. | 4x-y+4=0 | D. | 4x+y-4=0 |
6.已知i是虚数单位,则复数i(1+i)的共轭复数为( )
| A. | 1+i | B. | l-i | C. | -l+i | D. | -l-i |
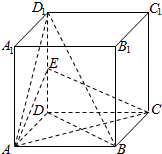 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.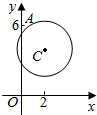 已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)
已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)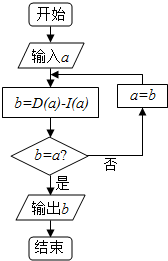 已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )