题目内容
4.如图,平行四边形ABCD中,AB=2AD=2,∠BAD=60°,E为DC的中点,那么$\overrightarrow{AC}$与$\overrightarrow{EB}$所成角的余弦值为( )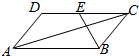
| A. | $\frac{\sqrt{7}}{7}$ | B. | -$\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{14}$ | D. | -$\frac{\sqrt{7}}{14}$ |
分析 建立平面直角坐标系,写出向量的坐标,代入夹角公式计算.
解答  解:以AB所在直线为x轴,A为原点,建立平面直角坐标系,如图,则A(0,0),B(2,0),C($\frac{5}{2}$,$\frac{\sqrt{3}}{2}$),D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),E($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
解:以AB所在直线为x轴,A为原点,建立平面直角坐标系,如图,则A(0,0),B(2,0),C($\frac{5}{2}$,$\frac{\sqrt{3}}{2}$),D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),E($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
∴$\overrightarrow{AC}$=($\frac{5}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{EB}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),∴|$\overrightarrow{AC}$|=$\sqrt{(\frac{5}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{7}$,|$\overrightarrow{EB}$|=$\sqrt{({\frac{1}{2})}^{2}+({-\frac{\sqrt{3}}{2})}^{2}}$=1.$\overrightarrow{AC}•\overrightarrow{EB}$=$\frac{5}{4}-\frac{3}{4}$=$\frac{1}{2}$.
∴cos<$\overrightarrow{AC},\overrightarrow{EB}$>=$\frac{\frac{1}{2}}{\sqrt{7}}$=$\frac{\sqrt{7}}{14}$.
故选:C.
点评 本题考查了平面向量的数量积运算在集合中的应用,建立平面直角坐标系是快捷解题方法之一.

练习册系列答案
相关题目
14.若函数$f(x)=sinωx-\sqrt{3}cosωx$,ω>0,x∈R,又f(x1)=2,f(x2)=0,且|x1-x2|的最小值为$\frac{3π}{2}$,则ω的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 2 |
13.函数f(x)=2x2-mx+3在(-∞,2)上的减函数,在(2,+∞)上是增函数,则m的值为( )
| A. | -2 | B. | -8 | C. | 2 | D. | 8 |