题目内容

16．已知命题p：?x∈R，ax2+2x+a≥0；命题q：a2-2a-3≤0，若命题p∧q为真命题，求a的取值范围．

分析 分别求出p，q为真时的a的范围，取交集即可．

解答 解：关于命题p：?x∈R，ax2+2x+a≥0，
则$\left\{\begin{array}{l}{a＞0}\\{△=4-{4a}^{2}≤0}\end{array}\right.$，解得：a＞1；
关于命题q：a2-2a-3≤0，
解得：-1≤a≤3，
若命题p∧q为真命题，
则p，q均为真命题，
故a的取值范围是（1，3]．

点评 本题考查了二次函数的性质，考查复合命题的判断，是一道基础题．

练习册系列答案
相关题目
6．在正方体ABCDD一A1B1C1D1中，点E为线段C1D1上一点，且满足$\frac{{D}_{1}E}{E{C}_{1}}$=$\sqrt{3}$+1，则直线AB1与直线CE所成的角的大小为（　　）
A．30°B．45°C．60°D．90°
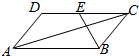
7．在△ABC中，角A，B，C所对边分别为a，b，c，且$c=4\sqrt{2}$，B=45°，面积S=2，则a=1；b=5．
4．如图，平行四边形ABCD中，AB=2AD=2，∠BAD=60°，E为DC的中点，那么$\overrightarrow{AC}$与$\overrightarrow{EB}$所成角的余弦值为（　　）
A．$\frac{\sqrt{7}}{7}$B．-$\frac{\sqrt{7}}{7}$C．$\frac{\sqrt{7}}{14}$D．-$\frac{\sqrt{7}}{14}$
11．设函数f（x）=|x-a|+|x|．
（Ⅰ）若a=1，解不等式f（x）＞2；
（Ⅱ）若存在x∈R，使得不等式f（x）$≤\frac{{t}^{2}+3}{t+1}$对任意t＞-1恒成立，求实数a的取值范围．
1．已知数列{an}满足：a1=$\frac{1}{2}$，an+1-an=p•3n-1-nq，n∈N*，p，q∈R．
（1）若q=0，且数列{an}为等比数列，求p的值；
（2）若p=1，且a4为数列{an}的最小项，求q的取值范围．
8．已知定义在R上的二次函数f（x）的图象过原点，且满足f（x+1）-f（x）=2x+2，函数g（x）=ax（a＞0，a≠1）．
（1）求f（x）的解析式；
（2）设h（x）=-f（x）+bx，当a=2时，若对任意x∈[1，2]，都存在x1，x2∈[1，2]，使得h（x）≤h（x1），g（x）≤g（x2），且h（x1）=g（x2），求实数b的值；
（3）若关于x的方程f（x）=g（2x）恰有一实数解x0，且x0∈（$\frac{1}{4}$，$\frac{1}{2}$），求实数a的取值范围．
5．给出下列命题，其中正确的命题个数是（　　）
①已知a＞0，b＞0，则$\frac{2ab}{a+b}$≤$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$；
②已知a＞0，b＞0，c＞0，则a+b+c≥$\sqrt{ab}$+$\sqrt{bc}$$+\sqrt{ac}$；
③已知x＞0，则函数f（x）=$\frac{{x}^{2}+1}{{x}^{2}-x+1}$的最大值为2；
④若x＞0，则ln（1+x）＞$\frac{x}{1+x}$．
A．1B．2C．3D．4
6．已知向量$\overrightarrow{a}$=（1，2，3），$\overrightarrow{b}$=（x，x2+y-2，y）并且$\overrightarrow{a}$，$\overrightarrow{b}$同向，则x，y的值为$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网