题目内容
15.在△ABC中,a、b分别为角A、B的对边,如果B=30°,C=105°,a=4,那么b=$2\sqrt{2}$.分析 利用正弦定理即可得出.
解答 解:在△ABC中,∵B=30°,C=105°,
∴A=45°.
由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,
∴b=$\frac{asinB}{sinA}$=$\frac{4sin3{0}^{°}}{sin4{5}^{°}}$=$\frac{4×\frac{1}{2}}{\frac{\sqrt{2}}{2}}$=$2\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了正弦定理、三角形内角和定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
6.在正方体ABCDD一A1B1C1D1中,点E为线段C1D1上一点,且满足$\frac{{D}_{1}E}{E{C}_{1}}$=$\sqrt{3}$+1,则直线AB1与直线CE所成的角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
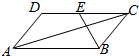
4.如图,平行四边形ABCD中,AB=2AD=2,∠BAD=60°,E为DC的中点,那么$\overrightarrow{AC}$与$\overrightarrow{EB}$所成角的余弦值为( )

| A. | $\frac{\sqrt{7}}{7}$ | B. | -$\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{14}$ | D. | -$\frac{\sqrt{7}}{14}$ |