题目内容
13.函数f(x)=2x2-mx+3在(-∞,2)上的减函数,在(2,+∞)上是增函数,则m的值为( )| A. | -2 | B. | -8 | C. | 2 | D. | 8 |
分析 若函数f(x)=2x2-mx+3在(-∞,2)上的减函数,在(2,+∞)上是增函数,则函数f(x)=2x2-mx+3的图象关于直线x=2对称,即$\frac{m}{4}$=2,解得答案.
解答 解:∵函数f(x)=2x2-mx+3在(-∞,2)上的减函数,在(2,+∞)上是增函数,
∴函数f(x)=2x2-mx+3的图象关于直线x=2对称,
即$\frac{m}{4}$=2,
解得:m=8,
故选:D
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.如图,平行四边形ABCD中,AB=2AD=2,∠BAD=60°,E为DC的中点,那么$\overrightarrow{AC}$与$\overrightarrow{EB}$所成角的余弦值为( )
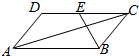

| A. | $\frac{\sqrt{7}}{7}$ | B. | -$\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{14}$ | D. | -$\frac{\sqrt{7}}{14}$ |