题目内容
已知sinα=3cosα,则(sinα+cosα)2= .
考点:三角函数中的恒等变换应用,三角函数的化简求值
专题:三角函数的求值
分析:利用同角三角函数基本关系和已知等式分别求得sin2α和cos2α代入(sinα+cosα)2中求得答案.
解答:
解:∵sinα=3cosα,
∴sin2α=9cos2α=9-9sin2α,
∴10sin2α=9,
∴sin2α=
,
∴cos2α=1-
=
∴(sinα+cosα)2=16cos2α=
=
,
故答案为:
∴sin2α=9cos2α=9-9sin2α,
∴10sin2α=9,
∴sin2α=
| 9 |
| 10 |
∴cos2α=1-
| 9 |
| 10 |
| 1 |
| 10 |
∴(sinα+cosα)2=16cos2α=
| 16 |
| 10 |
| 8 |
| 5 |
故答案为:
| 8 |
| 5 |
点评:本题主要考查了三角同角三角函数基本关系的应用,属于基础题.

练习册系列答案
相关题目
若平面内两个向量
=(2cosθ,1)与
=(1,cosθ)共线,则cos2θ等于( )
| a |
| b |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
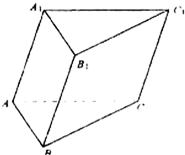 如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为
如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为