题目内容
已知函数f（x）=ax3+cx+d（a≠0）是R上的奇函数，且当x=1时取得极值-2，
（1）当x＞0时，求f（x）的单调区间；
（2）设g（x）=x4-2x2-3，对任意x∈[-
，
]都有f（x）≥g（x）成立，求实数a的取值范围．
（1）当x＞0时，求f（x）的单调区间；
（2）设g（x）=x4-2x2-3，对任意x∈[-
| 3 |
| 3 |
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：（1）利用导数判断函数的单调性，求出单调区间即可，注意对a进行讨论；
（2）由题意若对任意x∈[-
，
]都有f（x）≥g（x）成立，即f（x）min≥g（x）max，利用（1）的结论求得f（x）及g（x）的最值即可得出结论．
（2）由题意若对任意x∈[-
| 3 |
| 3 |
解答：
解：（1）由题意函数f（x）是奇函数得f（0）=0，∴d=0．又当x=1时取得极值，得f′（1）=0，∴c=-3a．
∴f（x）=ax3-3ax，（a≠0，x＞0）．f′（x）=3a（x+1）（x-1），
①若a＞0，f（x）在（0，1）递减，在（1，+∞）递增．
②若a＜0，f（x）在（0，1）递增，在（1，+∞）递减．
（2）由已知得g（x）=（x2-1）2-4，x2∈[0，3]，g（x）max=0，g（x）min=-4．
根据题意即f（x）min≥g（x）max=0，x∈[-
，
]
由（1）知，当a＞0时，f（x）min=min{f（-
），f（1）}=-2a＜0，
当a＜0时，f（x）min=min{f（-1），f（
））}=2a＜0．∴a∈Φ
∴f（x）=ax3-3ax，（a≠0，x＞0）．f′（x）=3a（x+1）（x-1），
①若a＞0，f（x）在（0，1）递减，在（1，+∞）递增．
②若a＜0，f（x）在（0，1）递增，在（1，+∞）递减．
（2）由已知得g（x）=（x2-1）2-4，x2∈[0，3]，g（x）max=0，g（x）min=-4．
根据题意即f（x）min≥g（x）max=0，x∈[-
| 3 |
| 3 |
由（1）知，当a＞0时，f（x）min=min{f（-
| 3 |
当a＜0时，f（x）min=min{f（-1），f（
| 3 |
点评：本题考查利用导数判断函数的单调性及求函数的最值等知识，以及不等式恒成立的条件问题，能把恒成立问题转化为求函数的最值问题，然后借助导数解决，体会分类讨论思想和转化划归思想的运用，属难题．
练习册系列答案
相关题目
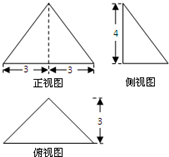如图是某个四面体的三视图，若在该四面体的外接球内任取一点，则点落在四面体内的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
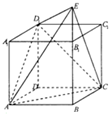如图长方体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形，E为BB1延长线上的一点且满足