题目内容
在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P所作的圆的两条切线相互垂直,则实数k的取值范围是 .
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意可得圆心为C(2,0),半径R=2;设两个切点分别为A、B,则由题意可得四边形PACB为正方形,圆心到直线y=k(x+1)的距离小于或等于PC=2
,
即
≤2
,由此求得k的范围.
| 2 |
即
| |2k-0+k| | ||
|
| 2 |
解答:
解:∵C的方程为x2+y2-4x=0,故圆心为C(2,0),半径R=2.
设两个切点分别为A、B,则由题意可得四边形PACB为正方形,故有PC=
R=2
,
∴圆心到直线y=k(x+1)的距离小于或等于PC=2
,
即
≤2
,解得k2≤8,可得-2
≤k≤2
,
故答案为:[-2
,2
].
设两个切点分别为A、B,则由题意可得四边形PACB为正方形,故有PC=
| 2 |
| 2 |
∴圆心到直线y=k(x+1)的距离小于或等于PC=2
| 2 |
即
| |2k-0+k| | ||
|
| 2 |
| 2 |
| 2 |
故答案为:[-2
| 2 |
| 2 |
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
二项式(x-1)n的奇数项二项式系数和64,若(x-1)n=a0+a1(x+1)+a2(x+1)2+…+an(x+1)n,则a1等于( )
| A、-14 | B、448 |
| C、-1024 | D、-16 |
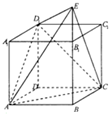 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,E为BB1延长线上的一点且满足
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,E为BB1延长线上的一点且满足 已知函数f(x)=2sin(ωx+φ)(其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是
已知函数f(x)=2sin(ωx+φ)(其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是